题目内容
设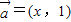 ,
,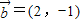 ,
,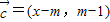 (x∈R,m∈R).
(x∈R,m∈R).(Ⅰ)若
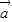 与
与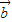 的夹角为钝角,求x的取值范围;
的夹角为钝角,求x的取值范围;(Ⅱ)解关于x的不等式
 .
.
【答案】分析:(1)根据已知中向量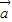 与
与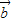 的坐标及
的坐标及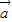 与
与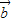 的夹角为钝角,根据向量数量积的定义,可得
的夹角为钝角,根据向量数量积的定义,可得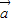 •
•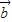 <0,由此可构造不等式,但要注意对向量反向情况的排除;
<0,由此可构造不等式,但要注意对向量反向情况的排除;
(2)根据 利用平方法可得
利用平方法可得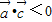 ,由此构造不等式,对m分类讨论后,综合讨论结果,可得答案.
,由此构造不等式,对m分类讨论后,综合讨论结果,可得答案.
解答:解:(1)∵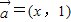 ,
,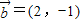 ,
,
若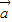 与
与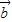 的夹角为钝角,
的夹角为钝角,
则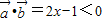 ,
,
解得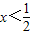 ;
;
又当x=-2时,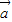 与
与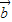 的夹角为π,
的夹角为π,
所以当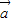 与
与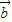 的夹角为钝角时,
的夹角为钝角时,
x的取值范围为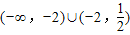 .…(6分)
.…(6分)
(2)由 知,
知,
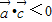 ,
,
又∵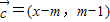
∴(x-1)[x-(m-1)]<0;…(8分)
当m<2时,解集为{x|m-1<x<1};…(10分)
当m=2时,解集为空集;…(12分)
当m>2时,解集为{x|1<x<m-1}.…(14分)
点评:本题考查的知识点是数量积,一元二次不等式的解法,其中(1)中易忽略当x=-2时,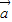 与
与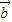 的夹角为π,而错解为
的夹角为π,而错解为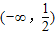
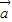 与
与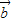 的坐标及
的坐标及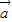 与
与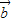 的夹角为钝角,根据向量数量积的定义,可得
的夹角为钝角,根据向量数量积的定义,可得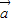 •
•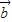 <0,由此可构造不等式,但要注意对向量反向情况的排除;
<0,由此可构造不等式,但要注意对向量反向情况的排除;(2)根据
 利用平方法可得
利用平方法可得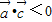 ,由此构造不等式,对m分类讨论后,综合讨论结果,可得答案.
,由此构造不等式,对m分类讨论后,综合讨论结果,可得答案.解答:解:(1)∵
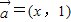 ,
,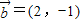 ,
,若
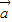 与
与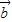 的夹角为钝角,
的夹角为钝角,则
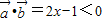 ,
,解得
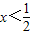 ;
;又当x=-2时,
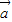 与
与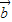 的夹角为π,
的夹角为π,所以当
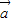 与
与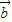 的夹角为钝角时,
的夹角为钝角时,x的取值范围为
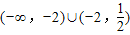 .…(6分)
.…(6分)(2)由
 知,
知,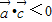 ,
,又∵
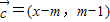
∴(x-1)[x-(m-1)]<0;…(8分)
当m<2时,解集为{x|m-1<x<1};…(10分)
当m=2时,解集为空集;…(12分)
当m>2时,解集为{x|1<x<m-1}.…(14分)
点评:本题考查的知识点是数量积,一元二次不等式的解法,其中(1)中易忽略当x=-2时,
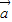 与
与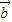 的夹角为π,而错解为
的夹角为π,而错解为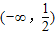

练习册系列答案
相关题目
 ,
, ,
, (x∈R,m∈R).
(x∈R,m∈R). 与
与 的夹角为钝角,求x的取值范围;
的夹角为钝角,求x的取值范围; .
. ,
, ,
, (x∈R,m∈R).
(x∈R,m∈R). 与
与 的夹角为钝角,求x的取值范围;
的夹角为钝角,求x的取值范围; .
.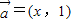 ,
,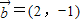 ,
,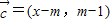 (x∈R,m∈R).
(x∈R,m∈R).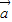 与
与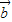 的夹角为钝角,求x的取值范围;
的夹角为钝角,求x的取值范围; .
.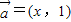 ,
,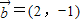 ,
,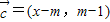 (x∈R,m∈R).
(x∈R,m∈R).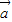 与
与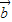 的夹角为钝角,求x的取值范围;
的夹角为钝角,求x的取值范围; .
.