题目内容
设函数f(x)=x2+aln(1+x)有两个极值点x1、x2,且x1<x2,
(Ⅰ)求a的取值范围,并讨论f(x)的单调性;
(Ⅱ)求f(x2)的取值范围。
(Ⅰ)求a的取值范围,并讨论f(x)的单调性;
(Ⅱ)求f(x2)的取值范围。
解:(Ⅰ)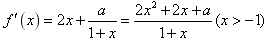 ,
,
令 ,
,
由题意知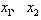 是方程g(x)=0的两个均大于-1的不相等的实根,
是方程g(x)=0的两个均大于-1的不相等的实根,
其充要条件为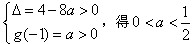 ,
,
(1)当 ,∴f(x)在
,∴f(x)在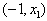 内为增函数;
内为增函数;
(2)当 ,∴f(x)在
,∴f(x)在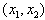 内为减函数;
内为减函数;
(3)当x∈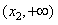 时,
时,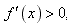 ,∴f(x)在
,∴f(x)在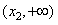 内为增函数;
内为增函数;
(Ⅱ)由(Ⅰ),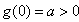 ,
,
∴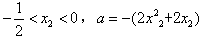 ,
,
∴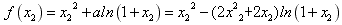 ,
,
设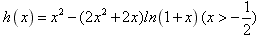 ,
,
则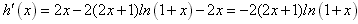 ,
,
(1)当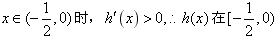 单调递增;
单调递增;
(2)当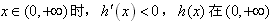 单调递减;
单调递减;
∴当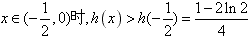 ,
,
故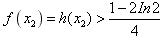 。
。
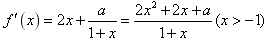 ,
,令
 ,
,由题意知
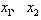 是方程g(x)=0的两个均大于-1的不相等的实根,
是方程g(x)=0的两个均大于-1的不相等的实根,其充要条件为
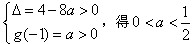 ,
,(1)当
 ,∴f(x)在
,∴f(x)在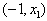 内为增函数;
内为增函数;(2)当
 ,∴f(x)在
,∴f(x)在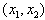 内为减函数;
内为减函数;(3)当x∈
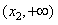 时,
时,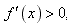 ,∴f(x)在
,∴f(x)在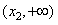 内为增函数;
内为增函数;(Ⅱ)由(Ⅰ),
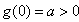 ,
,∴
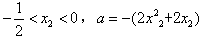 ,
,∴
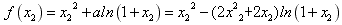 ,
,设
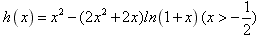 ,
,则
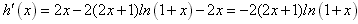 ,
,(1)当
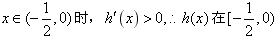 单调递增;
单调递增; (2)当
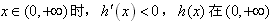 单调递减;
单调递减;∴当
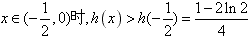 ,
,故
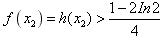 。
。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目