Question

从甲．乙两种树苗中各抽测10株树苗的高度，测出的高度如下：（单位：厘米）
甲：37，21，31，20，29，19，32，23，25，33；
乙：10，30，47，27，46，14，26，10，44，46
（1）根据抽测结果，完成如图1的茎叶图，并求甲．乙两种树苗高度的中位数和平均数；
（2）设抽测的10株甲树苗高度的平均值为

.

x

，用简单随机抽样的方法从10株乙种树苗中抽取1株，求抽到的树苗高度超过

.

x

的概率；
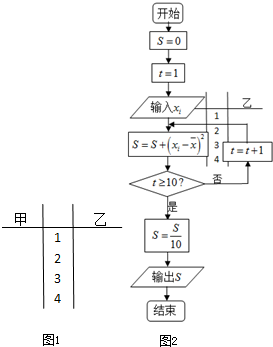
（3）将10株甲种树苗的高度依次输入如图2的程序框图进行运算，问输出的s大小为多少？并说明s的统计学意义．

Answer 1

分析：（1）用茎叶图表示两组数据，首先要先确定“茎”值，再将数据按“茎”值分组分类表示在“叶”的位置；利用数据，可计算甲、乙两种树苗高度的中位数和平均数；
（2）确定从10株乙种树苗中抽取1株，抽到的树苗高度超过

.

x

的个数，即可求概率；
（3）利用框图，可得结论．

解答：解：（1）茎叶图如图所示，甲的中位数是

25+28

2

=26.5，乙的中位数是

27+30

2

=28.5；
甲的平均数

37+21+31+20+29+19+32+23+25+33

10

=27，乙的平均数

10+30+47+27+46+14+26+10+44+46

10

=30；
（2）从10株乙种树苗中抽取1株，抽到的树苗高度超过

.

x

的，共有5个，
∴抽到的树苗高度超过

.

x

的概率为

5

10

=

1

2

；
（3）s=

1

10

•[（37-27）²+（21-27）²+（31-27）²+（20-27）²+（29-27）²+（19-27）²+（32-27）²+（23-27）²+（25-27）²+（33-27）²]=42.5
s的统计学意义是反映数据波动大小程度．

点评：本题考查框图，考查概率知识，考查学生的计算能力，属于中档题．