题目内容
设数列{an}的前n项和为Sn,且对任意正整数n,an+Sn=4096。
(1)求数列{an}的通项公式;
(2)设数列{log2an}的前n项和为Tn,对数列{Tn},从第几项起Tn<-509?
(1)求数列{an}的通项公式;
(2)设数列{log2an}的前n项和为Tn,对数列{Tn},从第几项起Tn<-509?
解:(1)∵an+Sn=4096,
∴a1+S1=4096,a1=2048,
当n≥2时,an=Sn-Sn-1=(4096-an)-(4096-an-1)=an-1-an,
∴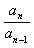 =
=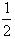 ,an=2048(
,an=2048(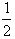 )n-1;
)n-1;
(2)∵log2an=log2[2048(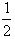 )n-1]=12-n,
)n-1]=12-n,
∴Tn=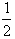 (-n2+23n),
(-n2+23n),
由Tn<-509,解得n>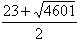 ,
,
而n是正整数,于是,n≥46,
∴从第46项起Tn<-509。
∴a1+S1=4096,a1=2048,
当n≥2时,an=Sn-Sn-1=(4096-an)-(4096-an-1)=an-1-an,
∴
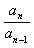 =
=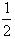 ,an=2048(
,an=2048(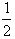 )n-1;
)n-1;(2)∵log2an=log2[2048(
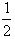 )n-1]=12-n,
)n-1]=12-n, ∴Tn=
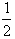 (-n2+23n),
(-n2+23n),由Tn<-509,解得n>
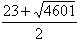 ,
,而n是正整数,于是,n≥46,
∴从第46项起Tn<-509。

练习册系列答案
相关题目