题目内容
一个长、宽、高分别为a、b、c长方体的体积是8cm2,它的全面积是32cm2,且满足 b2=ac,求这个长方体所有棱长之和.
分析:由长、宽、高分别为a、b、c长方体的体积是8cm2,知abc=8;由它的全面积是32cm2,知2(ab+bc+ca)=32,再由b2=ac,能求出这个长方体所有棱长之和.
解答:解:∵长、宽、高分别为a、b、c长方体的体积是8cm2,
∴abc=8,
∵它的全面积是32cm2,
∴2(ab+bc+ca)=32,
∵b2=ac,
∴b=2,ac=4,a+c=6,
∴这个长方体所有棱长之和为4(a+b+c)=32(cm).
∴abc=8,
∵它的全面积是32cm2,
∴2(ab+bc+ca)=32,
∵b2=ac,
∴b=2,ac=4,a+c=6,
∴这个长方体所有棱长之和为4(a+b+c)=32(cm).
点评:本题考查棱柱的结构特征的应用,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
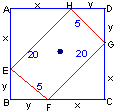 把一个长、宽、高分别为25cm、20cm、5cm的长方体木盒从一个正方形窗口穿过,那么正方形窗口的边长至少应为
把一个长、宽、高分别为25cm、20cm、5cm的长方体木盒从一个正方形窗口穿过,那么正方形窗口的边长至少应为