题目内容

不等式2|x|+|x-1|＜2的解集是________．

$\text{[math]}$
分析：由原不等式可得① $\text{[math]}$ ，或 ② $\text{[math]}$ ，或③ $\text{[math]}$ ，
所求不等式的解集是①②③解集的并集．
解答：不等式2|x|+|x-1|＜2；
即 ① $\text{[math]}$ ，或 ② $\text{[math]}$ ，或③ $\text{[math]}$ ，
解①得- $\text{[math]}$ ＜x＜0，解②得0≤x＜1，解③得 x∈∅，
故原不等式的解集是①②③解集的并集，故原不等式的解集为 $\text{[math]}$ ，
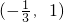故答案为： $\text{[math]}$ ．
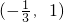点评：把绝对值不等式进行等价转化为与之等价的3个不等式组来解，体现了分类讨论的数学思想．

练习册系列答案

小学生学习指导丛书系列答案

课堂小测本系列答案

优秀生数法题解系列答案

亮点激活精编全能大试卷系列答案

成长背囊高效测评单元测试卷系列答案

伴你成长同步辅导与能力训练系列答案

黄冈金牌之路单元月考卷系列答案

伴你成长阶段综合测试卷集系列答案

红领巾乐园沈阳出版社系列答案

思维体操系列答案

相关题目

15、A．化极坐标方程ρ²cosθ-ρ=0为直角坐标方程为

x²+y²=0或x=1

．
B．不等式|2-x|+|x+1|≤a对任意x∈[0，5]恒成立的实数a的取值范围为

，5]，其中m是不等于零的常数，
（1）（理）写出h（4x）的定义域；
（文）m=1时，直接写出h（x）的值域；
（2）（文、理）求h（x）的单调递增区间；
（3）已知函数f（x）（x∈[a，b]），定义：f₁（x）=minf（t）|a≤t≤x（x∈[a，b]），f₂（x）=maxf（t）|a≤t≤x（x∈[a，b]）．其中，minf（x）|x∈D表示函数f（x）在D上的最小值，maxf（x）|x∈D表示函数f（x）在D上的最大值．例如：f（x）=cosx，x∈[0，π]，则f₁（x）=cosx，x∈[0，π]，f₂（x）=1，x∈[0，π]．
（理）当m=1时，设M(x)=

，不等式t≤M₁（x）-M₂（x）≤n恒成立，求t，n的取值范围；
（文）当m=1时，|h₁（x）-h₂（x）|≤n恒成立，求n的取值范围．

仔细阅读下面问题的解法：
设A=[0，1]，若不等式2^1-x+a＞0在A上有解，求实数a的取值范围．
解：令f（x）=2^1-x+a，因为f（x）＞0在A上有解．

⇒f(x)在A上的最大值大于0，

又∵f(x)在[0，1]上单调递减

⇒f(x)最大值=f(0)
=2+a＞0⇒a＞-2
学习以上问题的解法，解决下面的问题，已知：函数f（x）=x²+2x+3（-2≤x≤-1）．
①求f（x）的反函数f^-1（x）及反函数的定义域A；
②设B={x|lg

＞lg(2x+a-5)}，若A∩B≠∅，求实数a的取值范围．

（2013•渭南二模）（不等式选讲）不等式|2-x|+|x+1|＜a对于任意x∈[0，6]恒成立的实数a的集合为

A）选修4-1：几何证明选讲
如图，⊙O的割线PAB交⊙O于A，B两点，割线PCD经过圆心交⊙O于C，D两点，若PA=2，AB=4，PO=5，则⊙O的半径长为

．

（B）选修4-4：坐标系与参数方程
参数方程

中当t为参数时，化为普通方程为

x²-y²=1（x≥1）

x²-y²=1（x≥1）

．
（C）选修4-5：不等式选讲
不等式|2-x|+|x+1|≤a对于任意x∈[0，5]恒成立的实数a的集合为