题目内容
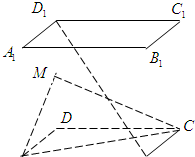在正方体ABCD-A1B1C1D1中，M为DD1中点．
（1）求AA1和BD1所成的角的余弦值．；
（2）求证：BD1∥平面ACM．
解：（1）设正方体的棱长为1，则∠D1BB1 即为AA1和BD1所成的角．
Rt△D1BB1中，cos∠D1BB1=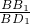
=
=
，即AA1和BD1所成的角的余弦值为 ．
（2）证明：设AC和 BD交与点O，又M为DD1中点，则由正方体的性质可得 OM 是三角形DBD1 的中位线，
∴OM∥BD1 ．而 OM?平面ACM，BD1 不在平面ACM内，故 BD1∥平面ACM．
分析：（1）设正方体的棱长为1，由正方体的性质可得∠D1BB1 即为AA1和BD1所成的角，Rt△D1BB1中，根据cos∠D1BB1=，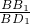
运算求得结果．
（2）设AC和 BD交与点O，又M为DD1中点，则由正方体的性质可得 OM 是三角形DBD1 的中位线，则有OM∥BD1，由此证得
BD1∥平面ACM．
点评：本题考查异面直线所成的角的定义和求法，直线和平面平行的判定方法，利用正方体的性质是解题的关键．
Rt△D1BB1中，cos∠D1BB1=
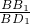==，即AA1和BD1所成的角的余弦值为 ．（2）证明：设AC和 BD交与点O，又M为DD1中点，则由正方体的性质可得 OM 是三角形DBD1 的中位线，
∴OM∥BD1 ．而 OM?平面ACM，BD1 不在平面ACM内，故 BD1∥平面ACM．
分析：（1）设正方体的棱长为1，由正方体的性质可得∠D1BB1 即为AA1和BD1所成的角，Rt△D1BB1中，根据cos∠D1BB1=
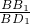，运算求得结果．
（2）设AC和 BD交与点O，又M为DD1中点，则由正方体的性质可得 OM 是三角形DBD1 的中位线，则有OM∥BD1，由此证得
BD1∥平面ACM．
点评：本题考查异面直线所成的角的定义和求法，直线和平面平行的判定方法，利用正方体的性质是解题的关键．
练习册系列答案
相关题目
16、在正方体ABCD-A′B′C′D′中，过对角线BD′的一个平面交AA′于E，交CC′于F，则
如图，在正方体ABCD-A′B′C′D′中，E，F分别是AB′，BC′的中点． 
如图在正方体ABCD-A 1B1C1D1中，O是底面ABCD的中心，B1H⊥D1O，H为垂足，则B1H与平面AD1C的位置关系是（ ）