Question

已知x+y=1，那么2x²+3y²的最小值是

1. A.
   
2. B.
   
3. C.
   
4. D.
   

Answer 1

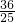
B
分析：法一：首先把x+y=1写成y=1-x，然后把y=1-x代入2x²+3y²中，在定义域的范围内求出函数的最值．
法二：欲求2x²+3y²的最小值，根据它与条件的结构特点，考虑利用柯西不等式解决．
解答：法一：x+y=1，
∴y=1-x，
∴令u=2x²+3y²=5x²-6x+3=5，
∴当x=时函数u有最小值，
u最小值=．
法二：因为x+y=1，
所以利用柯西不等式得
（2x²+3y²）[（）²+（）²]≥（x+y）²，
即（2x²+3y²）≥1，
即2x²+3y²≥，
当且仅当 即 时取等号，
即2x²+3y²的最小值为．
故选B．
点评：本题主要考查二次函数的最值的知识点，解答本题的关键是把y用x表示出来，代入式子中，求出函数的最值，本题也可以利用柯西不等式求最值，关键是利用：（2x²+3y²）[（）²+（）²]≥（x+y）²．