题目内容
已知函数f(x)=2 -2的反函数为f-1(x),各项均为正数的两个数列{an},{bn}满足:an= f(Sn),bn= f-1(n),其中Sn为数列{an}的前n项和,n∈N*,
-2的反函数为f-1(x),各项均为正数的两个数列{an},{bn}满足:an= f(Sn),bn= f-1(n),其中Sn为数列{an}的前n项和,n∈N*,
(1)求数列{an},{bn}的通项公式;
(2)若数列{cn}的前n项和为Tn,且 ,试比较Tn与
,试比较Tn与 的大小。
的大小。
 -2的反函数为f-1(x),各项均为正数的两个数列{an},{bn}满足:an= f(Sn),bn= f-1(n),其中Sn为数列{an}的前n项和,n∈N*,
-2的反函数为f-1(x),各项均为正数的两个数列{an},{bn}满足:an= f(Sn),bn= f-1(n),其中Sn为数列{an}的前n项和,n∈N*,(1)求数列{an},{bn}的通项公式;
(2)若数列{cn}的前n项和为Tn,且
 ,试比较Tn与
,试比较Tn与 的大小。
的大小。 解:(1)由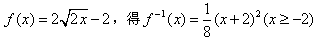 ,
,
∴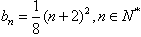 ,
,
由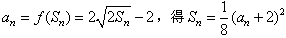 ,
,
当n=1时,得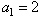 ;
;
当n≥2时,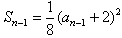 ,
,
∴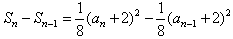 ,
,
∴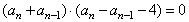 ,
,
∵an>0,
∴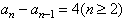 ,
,
∴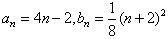 。
。
(2)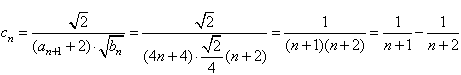 ,
,
∴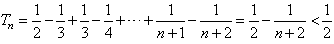 。
。
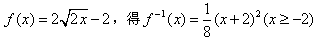 ,
,∴
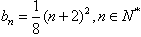 ,
,由
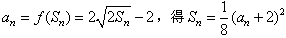 ,
,当n=1时,得
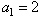 ;
;当n≥2时,
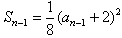 ,
,∴
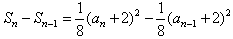 ,
,∴
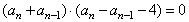 ,
,∵an>0,
∴
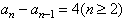 ,
, ∴
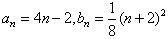 。
。(2)
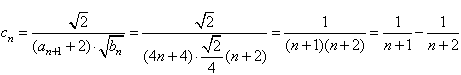 ,
,∴
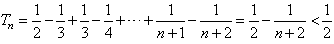 。
。 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目