题目内容

（理）已知向量 $数学公式$ =（1，0）， $数学公式$ =（0，1），向量 $数学公式$ 满足（ $数学公式$ •（ $数学公式$ ）=0，则| $数学公式$ |的最大值是________．

$\text{[math]}$
分析：设 $\text{[math]}$ =（m，n），由（ $\text{[math]}$ •（ $\text{[math]}$ ）=0得到 $\text{[math]}$ + $\text{[math]}$ = $\text{[math]}$ ，| $\text{[math]}$ |的最大值是此圆的直径．
解答：设 $\text{[math]}$ =（m，n），∵（ $\text{[math]}$ •（ $\text{[math]}$ ）=（m+1，n）•（m，n+1）=m²+m+n²+n
= $\text{[math]}$ + $\text{[math]}$ - $\text{[math]}$ =0，∴ $\text{[math]}$ + $\text{[math]}$ = $\text{[math]}$ ，
∴点（m，n）表示以（- $\text{[math]}$ ，- $\text{[math]}$ ）为圆心，半径等于 $\text{[math]}$ 的圆，且过原点．
故| $\text{[math]}$ |表示圆上的点与原点间的距离，故| $\text{[math]}$ |的最大值是圆的直径 $\text{[math]}$ ，
故答案为： $\text{[math]}$ ．
点评：本题考查两个向量的加减法的法则，以及其几何意义，两个向量的数量积公式的应用．
关键是弄清 $\text{[math]}$ + $\text{[math]}$ = $\text{[math]}$ 和| $\text{[math]}$ |所表示的几何意义．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

（理）已知向量

=（1，1），向量

=-1．
（1）求向量

；
（2）若向量

=（1，0）的夹角为

=（cosA，2cos2

），其中A、B、C为△ABC的内角a、b、c为三边，b²+ac=a²+c²，求|

|的取值范围．

（理）已知向量

=（1，0），

=（0，1），向量

|的最大值是

（2008•杨浦区二模）（理）已知向量

=(x2+1，-x)，

) （n为正整数），函数f(x)=

，设f（x）在（0，+∞）上取最小值时的自变量x取值为a_n．
（1）求数列{a_n}的通项公式；
（2）已知数列{b_n}，对任意正整数n，都有b_n•（4a_n²-5）=1成立，设S_n为数列{b_n}的前n项和，求

Sn；
（3）在点列A₁（1，a₁）、A₂（2，a₂）、A₃（3，a₃）、…、A_n（n，a_n）、…中是否存在两点A_i，A_j（i，j为正整数）使直线A_iA_j的斜率为1？若存在，则求出所有的数对（i，j）；若不存在，请你写出理由．

(2008海南、宁夏高考,理13)已知向量＝(0,-1,1), ＝(4,1,0),|λ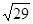+|＝,且λ＞0,则λ＝________________.

（理）已知向量

=（1，1），向量

=-1．
（1）求向量

；
（2）若向量

=（1，0）的夹角为

=（cosA，2cos2

），其中A、B、C为△ABC的内角a、b、c为三边，b²+ac=a²+c²，求|

|的取值范围．