题目内容
15.方程mx2+ny2=1不可能表示的曲线为( )| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
分析 根据方程mx2+ny2=1中不含有x(或y)的一次项,即可得出结论.
解答 解:∵方程mx2+ny2=1中不含有x(或y)的一次项,
∴方程mx2+ny2=1不可能表示抛物线,
故选:D.
点评 本题考查圆锥曲线的共同特征,考查抛物线方程,比较基础.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
6.曲线y=ex上的点到直线y=x的距离的最小值是( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{e}{2}$ | D. | $\frac{{\sqrt{e}}}{2}$ |
5.一个物体的运动方程为s(t)=sint,则它在$t=\frac{π}{3}$时的速度为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{π}{3}$ |
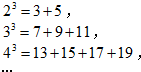 已知大于1的任意一个自然数的三次幂都可写成连续奇数的和.如:
已知大于1的任意一个自然数的三次幂都可写成连续奇数的和.如: