题目内容
已知x2+x≤6,求 的最大值和最小值,并求相应的x的值.
的最大值和最小值,并求相应的x的值.
解:由x2+x≤6,得-3≤x≤2…(2分)
令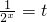 ,则
,则 …(2分)
…(2分)
 =
= …(2分)
…(2分)
则当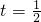 ,
, ,此时x=1;…(3分)
,此时x=1;…(3分)
当t=8,ymax=57,此时x=-3;…(3分)
分析:由题意,先解一元二次不等式x2+x≤6,得出函数 的定义域,再令
的定义域,再令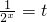 用换元法将此函数变为二次函数,利用二次函数的性质求出最值,再由此时t的取值求出相应的x的值
用换元法将此函数变为二次函数,利用二次函数的性质求出最值,再由此时t的取值求出相应的x的值
点评:本题考查二次函数在闭区间上的最值,解题的关键是利用换元法将指数型函数转化为二次函数,再由二次函数的性质求出最值,利用换元法转化是本题的重点,换元后求出新元t的取值范围是解题的难点,换元法是一种非常重要的技巧,由于其变换后使得解析式大大简化,方便了解题,故在求函数值域及最值时应用非常广泛.
令
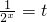 ,则
,则 …(2分)
…(2分) =
= …(2分)
…(2分)则当
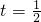 ,
, ,此时x=1;…(3分)
,此时x=1;…(3分)当t=8,ymax=57,此时x=-3;…(3分)
分析:由题意,先解一元二次不等式x2+x≤6,得出函数
 的定义域,再令
的定义域,再令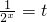 用换元法将此函数变为二次函数,利用二次函数的性质求出最值,再由此时t的取值求出相应的x的值
用换元法将此函数变为二次函数,利用二次函数的性质求出最值,再由此时t的取值求出相应的x的值点评:本题考查二次函数在闭区间上的最值,解题的关键是利用换元法将指数型函数转化为二次函数,再由二次函数的性质求出最值,利用换元法转化是本题的重点,换元后求出新元t的取值范围是解题的难点,换元法是一种非常重要的技巧,由于其变换后使得解析式大大简化,方便了解题,故在求函数值域及最值时应用非常广泛.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的最大值和最小值,并求相应的x的值.
的最大值和最小值,并求相应的x的值.