题目内容
已知向量 ,
, ,
, ,函数
,函数 .
.
(1)求函数 的表达式;
的表达式;
(2)求 的值;
的值;
(3)若 ,
, ,求
,求 的值.
的值.
 ,
, ,
, ,函数
,函数 .
.(1)求函数
 的表达式;
的表达式;(2)求
 的值;
的值;(3)若
 ,
, ,求
,求 的值.
的值.(1) (2)
(2) (3)
(3)
 (2)
(2) (3)
(3)
试题分析:
(1)利用两向量内积的坐标计算公式(两向量的横纵坐标对应相乘再相加)即可得到
 的函数解析式.
的函数解析式.(2)由(1)可得
 的函数解析式,把
的函数解析式,把 带入函数
带入函数 即可得到
即可得到 的值.
的值.(3)把等式
 带入
带入 ,利用诱导公式(奇变偶不变符号看象限)化简等式即可得到
,利用诱导公式(奇变偶不变符号看象限)化简等式即可得到 的值,正余弦的关系即可求出
的值,正余弦的关系即可求出 的值,再把
的值,再把 带入函数
带入函数 即可得到
即可得到 ,再利用和差角和倍角公式展开
,再利用和差角和倍角公式展开 并把
并把 的值带入即可得到
的值带入即可得到 的值.
的值.试题解析:
(1)∵
 ,
, ,
, ,
,∴
 ,即函数
,即函数 . (3分)
. (3分)(2)
 (6分)
(6分)(3)∵
 ,
,又
 ,∴
,∴ ,即
,即 . (7分)
. (7分)∵
 ,∴
,∴ . (8分)
. (8分)∴
 , (9分)
, (9分) . (10分)
. (10分)∴
 (11分)
(11分) . (12分)
. (12分)
练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
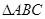 中,角
中,角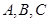 的对边分别为
的对边分别为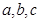 ,
,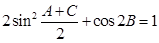
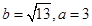 ,求
,求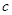 的值;
的值; 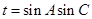 ,当
,当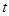 取最大值时求
取最大值时求 的值。
的值。 ”为假命题,则实数
”为假命题,则实数 的取值范围 ;
的取值范围 ; 均为锐角,且
均为锐角,且 ,则
,则 的大小关系为 ( )
的大小关系为 ( )


 ,tan
,tan =
= ,则cosβ=________.
,则cosβ=________. ≤α≤
≤α≤ ,则
,则 =________.
=________. ,且
,且 ,则
,则 的是( )
的是( )



 ,
, ,则
,则 的值是____________.
的值是____________. ,
, ,则
,则 的值等于________.
的值等于________.