题目内容
已知数列{an}满足a1=a，an=an+1+2．定义数列{bn}，使得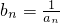
，n∈N*．若4＜a＜6，则数列{bn}的最大项为
- A.b2
- B.b3
- C.b4
- D.b5
B
分析：由题设知数列{an}是首项为a1=a，公差为d=an+1-an=2的等差数列，故bn=
，由此能求出数列{bn}的最大项．
解答：∵数列{an}满足a1=a，an=an+1+2，
∴数列{an}是首项为a1=a，公差为d=an+1-an=-2的等差数列，
∴
=-n2+（a-1）n是减数列，
∵4＜a＜6，
∴an=-n2+（a-1）n的最后一个正项是a3=3a-12，
∴bn=中，当n=3时，数列{bn}取最大项b3．
故选B．
点评：本题考查等差数列的性质和数列的函数特性质的应用，解题时要认真审题，注意数列的递推公式的灵活运用．
分析：由题设知数列{an}是首项为a1=a，公差为d=an+1-an=2的等差数列，故bn=
，由此能求出数列{bn}的最大项．解答：∵数列{an}满足a1=a，an=an+1+2，
∴数列{an}是首项为a1=a，公差为d=an+1-an=-2的等差数列，
∴
=-n2+（a-1）n是减数列，∵4＜a＜6，
∴an=-n2+（a-1）n的最后一个正项是a3=3a-12，
∴bn=
中，当n=3时，数列{bn}取最大项b3．故选B．
点评：本题考查等差数列的性质和数列的函数特性质的应用，解题时要认真审题，注意数列的递推公式的灵活运用．
练习册系列答案
相关题目