题目内容
 如图,B、A是某海面上位于东西方向相距30
如图,B、A是某海面上位于东西方向相距30| 2 |
| 3 |
分析:先根据内角和求得求得∠BAC,在△ABC中利用正弦定理求得AC的长,在△ABD中利用正弦定理求得AD的长,在△ACD中利用余弦定理求得DC的长,进而利用里程除以速度即可求得时间.
解答:解:在△ABC中,AB=30
,∠ABC=90°,∠BAC=90°-45°=45°
∴AC=
=60…(4分)
在△ABD中,∠DAB=15°+90°=105°,∠ABD=90°-60°=30°,∴∠ADB=45°
由正弦定理,得
=
∴AD=
=30…(9分)
在△ACD中,由余弦定理得DC2=AC2+AD2-2AC•AD•cos∠DAC=602+302-2×60×30×cos60°=2700
∴DC=30
…(12分)
则需要的时间t=
=1.5(小时)…(13分)
答:该救援船到达点C需要1.5小时…14分)
| 2 |
∴AC=
| AB |
| sin45° |
在△ABD中,∠DAB=15°+90°=105°,∠ABD=90°-60°=30°,∴∠ADB=45°
由正弦定理,得
| AD |
| sin∠ABD |
| AB |
| sin∠ADB |
30
| ||
| sin45° |
在△ACD中,由余弦定理得DC2=AC2+AD2-2AC•AD•cos∠DAC=602+302-2×60×30×cos60°=2700
∴DC=30
| 3 |
则需要的时间t=
30
| ||
20
|
答:该救援船到达点C需要1.5小时…14分)
点评:本题主要考查了解三角形的实际应用.考查了学生运用所学知识解决实际问题的能力.

练习册系列答案
相关题目
 海里的两个观测点。现位于B点正北方向、A点北偏东
海里的两个观测点。现位于B点正北方向、A点北偏东 方向的C点有一艘轮船发出求救信号,位于B点北偏西
方向的C点有一艘轮船发出求救信号,位于B点北偏西 、A点北偏西
、A点北偏西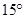 的D点的救援船立即前往营救,其航行速度为
的D点的救援船立即前往营救,其航行速度为 海里/小时.问该救援船到达C点需要多少时间?
海里/小时.问该救援船到达C点需要多少时间?
 海里的两个观测点。现位于B点正北方向、A点北偏东
海里的两个观测点。现位于B点正北方向、A点北偏东 方向的C点有一艘轮船发出求救信号,位于B点北偏西
方向的C点有一艘轮船发出求救信号,位于B点北偏西 、A点北偏西
、A点北偏西 的D点的救援船立即前往营救,其航行速度为
的D点的救援船立即前往营救,其航行速度为 海里/小时。问该救援船到达C点需要多少时间?
海里/小时。问该救援船到达C点需要多少时间?
 如图,B、A是某海面上位于东西方向相距
如图,B、A是某海面上位于东西方向相距 海里的两个观测点.现位于B点正北方向、A点北偏东45°方向的C点有一艘轮船发出求救信号,位于B点北偏西60°、A点北偏西15°的D点的救援船立即前往营救,其航行速度为
海里的两个观测点.现位于B点正北方向、A点北偏东45°方向的C点有一艘轮船发出求救信号,位于B点北偏西60°、A点北偏西15°的D点的救援船立即前往营救,其航行速度为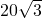 海里/小时.问该救援船到达C点需要多少时间?
海里/小时.问该救援船到达C点需要多少时间? 如图,B、A是某海面上位于东西方向相距
如图,B、A是某海面上位于东西方向相距 海里的两个观测点.现位于B点正北方向、A点北偏东45°方向的C点有一艘轮船发出求救信号,位于B点北偏西60°、A点北偏西15°的D点的救援船立即前往营救,其航行速度为
海里的两个观测点.现位于B点正北方向、A点北偏东45°方向的C点有一艘轮船发出求救信号,位于B点北偏西60°、A点北偏西15°的D点的救援船立即前往营救,其航行速度为 海里/小时.问该救援船到达C点需要多少时间?
海里/小时.问该救援船到达C点需要多少时间?