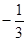题目内容
“a>1或b>1”是“a+b>2”的
必要不充分
必要不充分
条件.分析:原命题不好判断,可利用逆否命题的等价性,利用充分条件和必要条件的定义判断命题的逆否命题之间的关系即可.
解答:解:要判断“a>1或b>1”和“a+b>2”的条件关系,只需要判断“a+b≤2”和a≤1且b≤1的条件关系即可.
当a+b≤2时,比如当a=
,b=
时,满足a+b≤2,但a≤1且b≤1不成立.
若a≤1且b≤1,则必有a+b≤2,成立,
所以“a+b≤2”是a≤1且b≤1的必要不充分条件,
即“a>1或b>1”是“a+b>2”的必要不充分条件.
故答案为:必要不充分.
当a+b≤2时,比如当a=
| 3 |
| 2 |
| 1 |
| 2 |
若a≤1且b≤1,则必有a+b≤2,成立,
所以“a+b≤2”是a≤1且b≤1的必要不充分条件,
即“a>1或b>1”是“a+b>2”的必要不充分条件.
故答案为:必要不充分.
点评:本题主要考查充分条件和必要条件的判断,由于正面判断不好判断,则利用逆否命题的等价性,判断a+b≤2”和a≤1且b≤1的条件关系是解决本题的关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
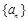 是公比为q的等比数列,且
是公比为q的等比数列,且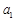 ,
,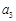 ,
,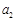 成等差数列,则q=
成等差数列,则q=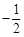 B.1 C.
B.1 C. 展开式中常数项为1120,其中实数a是常数,则展开式中各项系数的和是
展开式中常数项为1120,其中实数a是常数,则展开式中各项系数的和是 B.1或
B.1或 C.
C.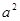 与
与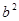 的等比中项,又是
的等比中项,又是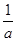 与
与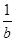 的等差中项,则
的等差中项,则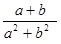 的值
的值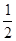 B、1或
B、1或 C、1或
C、1或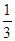 D、1或
D、1或