题目内容
对向量a=(a1,a2),b=(b1,b2)定义一种运算“?”:a?b=(a1,a2)?(b1,b2)=(a1b1,a2b2),已知动点P、Q分别在曲线y=sinx和y=f(x)上运动,且
=
?
+
(其中为O坐标原点),若
=(
,3),
=(
,0),则y=f(x)的最大值为( )
| OQ |
| m |
| OP |
| n |
| m |
| 1 |
| 2 |
| n |
| π |
| 6 |
分析:根据所给的运算整理要求解的结论,得到y=f(x)的表示式,后面的问题变为通过恒等变形进行三角函数性质的应用.
解答:解:设p点的坐标是(x,sinx)
∵
=
?
+
=(
x,3sinx)+(
π,0)
=(
x+
π,3sinx),
∵点Q在y=f(x)的图象上运动,
∴y=3sin(
x+
π)
∴函数的最大值为3
故选C
∵
| OQ |
| m |
| OP |
| n |
| 1 |
| 2 |
| 1 |
| 6 |
=(
| 1 |
| 2 |
| 1 |
| 6 |
∵点Q在y=f(x)的图象上运动,
∴y=3sin(
| 1 |
| 2 |
| 1 |
| 6 |
∴函数的最大值为3
故选C
点评:新定义类型的试题的解题关键在于体会思路的形成过程、数学思想方法的应用,发现解题方法,总结解题规律,从而提高学生综合应用知识分析和解决问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
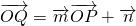 (其中为O坐标原点),若
(其中为O坐标原点),若  的最大值为
的最大值为

 (其中为O坐标原点),若
(其中为O坐标原点),若  的最大值为( )
的最大值为( )

 (其中为O坐标原点),若
(其中为O坐标原点),若  的最大值为( )
的最大值为( )
