题目内容
已知向量 =(2sinx,
=(2sinx, cosx),
cosx), =(sinx,2sinx),函数f(x)=
=(sinx,2sinx),函数f(x)= •
• .
.
(Ⅰ)求f(x)的单调递增区间;
(Ⅱ)若不等式f(x)≥m对x∈[0, ]都成立,求实数m的最大值.
]都成立,求实数m的最大值.
解:(Ⅰ)∵向量 =(2sinx,
=(2sinx, cosx),
cosx), =(sinx,2sinx),函数f(x)=
=(sinx,2sinx),函数f(x)= •
• .
.
∴f(x)=2sin2x+2 sinxcosx=
sinxcosx= sin2x-cos2x+1=2sin(2x-
sin2x-cos2x+1=2sin(2x- )+1
)+1
∴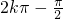 ≤2x-
≤2x- ≤
≤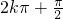 (k∈Z)
(k∈Z)
∴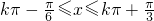 (k∈Z)
(k∈Z)
∴f(x)的单调递增区间为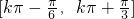 (k∈Z);
(k∈Z);
(Ⅱ)不等式f(x)≥m对x∈[0, ]都成立,即f(x)min≥m成立
]都成立,即f(x)min≥m成立
∵x∈[0, ],∴2x-
],∴2x- ∈
∈
∴sin(2x- )∈
)∈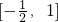
∴f(x)=2sin(2x- )+1∈[0,3]
)+1∈[0,3]
∴m≤0
∴m的最大值为0.
分析:(Ⅰ)根据向量 =(2sinx,
=(2sinx, cosx),
cosx), =(sinx,2sinx),函数f(x)=
=(sinx,2sinx),函数f(x)= •
• ,利用向量的数量积公式,结合二倍角、辅助角公式化简函数,从而可得f(x)的单调递增区间;
,利用向量的数量积公式,结合二倍角、辅助角公式化简函数,从而可得f(x)的单调递增区间;
(Ⅱ)不等式f(x)≥m对x∈[0, ]都成立,即f(x)min≥m成立.
]都成立,即f(x)min≥m成立.
点评:本题考查向量的数量积运算,考查函数的单调性,考查恒成立问题,正确确定函数解析式是关键.
 =(2sinx,
=(2sinx, cosx),
cosx), =(sinx,2sinx),函数f(x)=
=(sinx,2sinx),函数f(x)= •
• .
.∴f(x)=2sin2x+2
 sinxcosx=
sinxcosx= sin2x-cos2x+1=2sin(2x-
sin2x-cos2x+1=2sin(2x- )+1
)+1∴
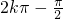 ≤2x-
≤2x- ≤
≤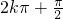 (k∈Z)
(k∈Z)∴
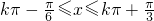 (k∈Z)
(k∈Z)∴f(x)的单调递增区间为
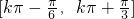 (k∈Z);
(k∈Z);(Ⅱ)不等式f(x)≥m对x∈[0,
 ]都成立,即f(x)min≥m成立
]都成立,即f(x)min≥m成立∵x∈[0,
 ],∴2x-
],∴2x- ∈
∈
∴sin(2x-
 )∈
)∈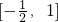
∴f(x)=2sin(2x-
 )+1∈[0,3]
)+1∈[0,3]∴m≤0
∴m的最大值为0.
分析:(Ⅰ)根据向量
 =(2sinx,
=(2sinx, cosx),
cosx), =(sinx,2sinx),函数f(x)=
=(sinx,2sinx),函数f(x)= •
• ,利用向量的数量积公式,结合二倍角、辅助角公式化简函数,从而可得f(x)的单调递增区间;
,利用向量的数量积公式,结合二倍角、辅助角公式化简函数,从而可得f(x)的单调递增区间;(Ⅱ)不等式f(x)≥m对x∈[0,
 ]都成立,即f(x)min≥m成立.
]都成立,即f(x)min≥m成立.点评:本题考查向量的数量积运算,考查函数的单调性,考查恒成立问题,正确确定函数解析式是关键.

练习册系列答案
相关题目
 =(2sinωx,cos2ωx),向量
=(2sinωx,cos2ωx),向量 =(cosωx,
=(cosωx, ),其中ω>0,函数f(x)=
),其中ω>0,函数f(x)= •
• ,若f(x)图象的相邻两对称轴间的距离为π.
,若f(x)图象的相邻两对称轴间的距离为π. ,恒有|f(x)-m|<2成立,求实数m的取值范围.
,恒有|f(x)-m|<2成立,求实数m的取值范围. =(2cosα,2sinα),
=(2cosα,2sinα),  =(3cosβ,3sinβ),若
=(3cosβ,3sinβ),若 与圆
与圆 的位置关系是( )
的位置关系是( )