Question

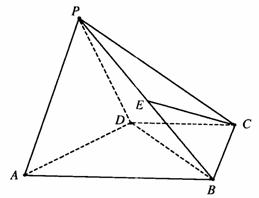
如图，在四棱锥P―ABCD中，平面PAD⊥平面ABCD，∠ABC=∠BCD=90°，PA=PD=DC=CD=E是BP的中点.

   （Ⅰ）求证：EC//平面APD；

   （Ⅱ）求BP与平面ABCD所成角的正切值；

   （Ⅲ）求二面角P―AB―D的大小.

Answer 1

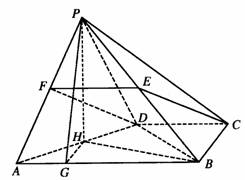
解法一：（Ⅰ）如图，取PA中点，连结EF、FD

∵E是BP的中点，

∴EF//AB且EF=AB

又∵DC//AB，DC=AB，

∴EF//CD且EF=CD

∴四边形EFDC是平行四边形，故得EC//FD

又∵EC平面PAD，FD平面PAD

∴EC//平面ADP

（Ⅱ）取AD中点H，连结PH，BH，因为PA=PD，

∴PH⊥AD

∵平面PAD⊥平面ABCD

∴PH⊥平面 ABCD

∴HB是PB在平面ABCD内的射影

∴∠PBH是PB与平面ABCD所成的角

由已知∠ABC=∠BCD=90°

∴四边形ABCD是直角梯形

DC=CB=AB

设AB=2a，则BD=a，在△ADB中，易得∠DBA=45°

∴AD=a

PH=

又∵

∴△ABD是等腰直角三角形，∠ADB=90°

∴HB=

∴在Rt△PHB中，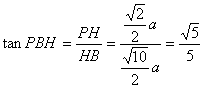

（Ⅲ）在平面ABCD内过点H作AB的垂线交于AB于G点，连结PG，则HG是PG在平面ABCD内的射影，故PG⊥AB，所以∠PGH是二面角P―AB―D的平面角，由AB=2a

HA=，又∠HAB=45°

∴HG=a

在Rt△PHG中，、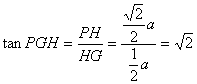

∴二面角P―AB―D的大小为

解法二：

（Ⅰ）同解法一

（Ⅱ）设AB=2a，同解法一中的（Ⅱ）

可得∠ADB=90°

如图，以D点为原点，DA所在直线为x轴，

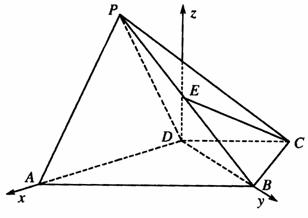
DB所在直线为y轴，过D点且垂直于平面

ABCD的直线与z轴建立空间直角坐标系.

则B=（0，0），P

平面ABCD的一个法向量为

所以，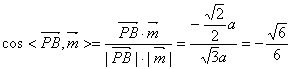

可得PB与平面ABCD所成角的正弦值为

所以PB与平面ABCD所成角的正切值为

（Ⅲ）易知设平面PAB的一个法向量，

则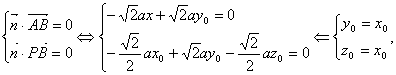

令=1，可得

得

所以二面角P―AB―D的大小为