题目内容

已知某圆的极坐标方程为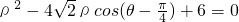 $数学公式$ ，若点P（x，y）在该圆上，则 $数学公式$ 的最大值是________．

$\text{[math]}$
分析：先把圆的极坐标方程化为直角坐标方程，进而利用直线与圆相切的意义即可求出．
解答：由圆的极坐标方程为 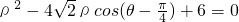$\text{[math]}$ 展开为ρ²-4ρcosθ-4ρsinθ+6=0，
化为x²+y²-4x-4y+6=0，即（x-2）²+（y-2）²=2，圆心C（2，2），半径r= $\text{[math]}$ ．
设 $\text{[math]}$ ，则y=kx．
当上述直线与圆相切时，得 $\text{[math]}$ ，化为k²-4k+1=0，解得 $\text{[math]}$ ．
由直线与圆相切的意义可知： $\text{[math]}$ 的最大值是 $\text{[math]}$ ．
故答案为 $\text{[math]}$ ．
点评：熟练掌握极坐标方程与直角坐标方程的互化及直线与圆相切的意义是解题的关键．

练习册系列答案

寒假总动员合肥工业大学出版社系列答案

寒假最佳学习方案寒假作业系列答案

寒假作业长江出版社系列答案

寒假作业黄山书社系列答案

寒假作业安徽教育出版社系列答案

寒假作业深圳报业集团出版社系列答案

寒假作业内蒙古人民出版社系列答案

寒假作业人民教育出版社系列答案

寒假作业云南人民出版社系列答案

寒假作业宁夏人民教育出版社系列答案

相关题目

在A，B，C，D四小题中只能选做2题，每题10分，共计20分．
A、如图，AB为⊙O的直径，BC切⊙O于B，AC交⊙O于P，CE=BE，E在BC上．求证：PE是⊙O的切线．
B、设M是把坐标平面上的点的横坐标伸长到2倍，纵坐标伸长到3倍的伸压变换．
（1）求矩阵M的特征值及相应的特征向量；
（2）求逆矩阵M^-1以及椭圆

=1在M^-1的作用下的新曲线的方程．
C、已知某圆的极坐标方程为：ρ2-4

)+6=0．
（Ⅰ）将极坐标方程化为普通方程；并选择恰当的参数写出它的参数方程；
（Ⅱ）若点P（x，y）在该圆上，求x+y的最大值和最小值．
D、若关于x的不等式|x+2|+|x-1|≥a的解集为R，求实数a的取值范围．

已知某圆的极坐标方程为ρ²-4

）+6=0．
（1）将极坐标方程化为普通方程，并选择恰当的参数写出它的参数方程；
（2）若点P（x，y）在该圆上，求x+y的最大值和最小值．（5分）

（1）已知某圆的极坐标方程为：ρ2-42ρcos（θ-π4）+6=0．将极坐标方程化为普通方程；并选择恰当的参数写出它的参数方程．
（2）已知二阶矩阵M有特征值λ=8及对应的一个特征向量e₁=

，且矩阵M对应的变换将点（-1，2）变换成
（-2，4）．求矩阵M的另一个特征值及对应的一个特征向量e2的坐标之间的关系．

已知某圆的极坐标方程为：ρ²-4

）+6=0．
（1）将极坐标方程化为普通方程；并选择恰当的参数写出它的参数方程；
（2）若点P（x，y）在该圆上，求x+y的最大值和最小值．

（2012•海口模拟）已知某圆的极坐标方程是p2-4

)+6=0
求：
（1）求圆的普通方程和一个参数方程；
（2）圆上所有点（x，y）中xy的最大值和最小值．