题目内容
如果函数f(x)对任意的实数x,存在常数M,使得不等式|f(x)|≤M|x|恒成立,那么就称函数f(x)为有界泛函数,下面四个函数:①f(x)=1;②f(x)=x2;③f(x)=(sinx+cosx)x;④f(x)=
其中属于有界泛函数的是( )
| x |
| x2+x+1 |
其中属于有界泛函数的是( )
| A.①② | B.①③ | C.③④ | D.②④ |
函数f(x)对任意的实数x,存在常数M,使得不等式|f(x)|≤M|x|恒成立,那么就称函数f(x)为有界泛函数,
∴①取x=0,则|f(x)|=1,|x|=0,故不存在常数M,使得不等式|f(x)|≤M|x|成立,因此①不是有界泛函数;
②若f(x)=x2是有界泛函数,则x2≤M|x|,取x=M+1,则有(M+1)2>M(M+1),故与假设矛盾,因此②不是有界泛函数;
③f(x)=(sinx+cosx)x≤
|x|,故③是有界泛函数;
④f(x)=
≤
|x|,故④是有界泛函数;
故选C.
∴①取x=0,则|f(x)|=1,|x|=0,故不存在常数M,使得不等式|f(x)|≤M|x|成立,因此①不是有界泛函数;
②若f(x)=x2是有界泛函数,则x2≤M|x|,取x=M+1,则有(M+1)2>M(M+1),故与假设矛盾,因此②不是有界泛函数;
③f(x)=(sinx+cosx)x≤
| 2 |
④f(x)=
| x |
| x2+x+1 |
| 4 |
| 3 |
故选C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
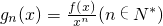 .若对定义域内的每一个x,总有gn(x)<0,则称f(x)为“n阶负函数”;若对定义域内的每一个x,总有
.若对定义域内的每一个x,总有gn(x)<0,则称f(x)为“n阶负函数”;若对定义域内的每一个x,总有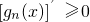 ,则称f(x)为“n阶不减函数”(
,则称f(x)为“n阶不减函数”(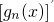 为函数gn(x)的导函数).
为函数gn(x)的导函数).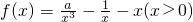 既是“1阶负函数”,又是“1阶不减函数”,求实数a的取值范围;
既是“1阶负函数”,又是“1阶不减函数”,求实数a的取值范围;