题目内容
3.已知实数集R,集合A={x|-2<x<3},集合B={x|x-a>0}.(Ⅰ)当a=1时,求(∁RA)∪B;
(Ⅱ)设A⊆B,求实数a的取值范围.
分析 (Ⅰ)当a=1时,B={x|x>1},A={x|-2<x<3},则CRA={x|x≤-2或x≥3},由此能求出(CRA)∪B.
(Ⅱ)由A={x|-2<x<3},B={x|x>a},利用A⊆B,能求出a的取值范围.
解答 解:(Ⅰ)当a=1时,B={x|x>1}.
∵A={x|-2<x<3}
∴∁RA={x|x≤-2或x≥3},
故(∁RA)∪B={x|x≤-2或x>1}…(4分)
(Ⅱ)∵A={x|-2<x<3},B={x|x>a},A⊆B,∴a≤-2
故实数a的取值范围为(-∞,-2]…(8分)
点评 本题考查集合的交、并、补集的混合运算,是基础题.解题时认真审题,仔细解答.

练习册系列答案
相关题目
13.函数$f(x)=\sqrt{3x-{x^2}}$的定义域为( )
| A. | [-3,0] | B. | (-∞,-3]∪[0,+∞) | C. | [0,3] | D. | (-∞,0]∪[3,+∞) |
18.执行如图所示的程序框图,如果输入a=-1,b=-2,则输出的a的值为( )


| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
12.执行如图所示的程序框图,输出的S值为( )
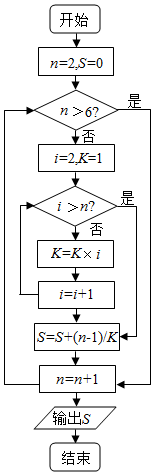

| A. | $\frac{119}{120}$ | B. | $\frac{359}{360}$ | C. | $\frac{719}{720}$ | D. | $\frac{5039}{5040}$ |
13.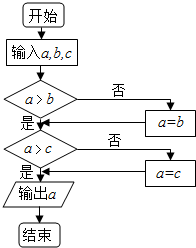 已知:a,b,c为集合A={1,2,3,4,5}中三个不同的数,通过如框图给出的一个算法输出一个整数a,则输出的数a=4的概率是( )
已知:a,b,c为集合A={1,2,3,4,5}中三个不同的数,通过如框图给出的一个算法输出一个整数a,则输出的数a=4的概率是( )
 已知:a,b,c为集合A={1,2,3,4,5}中三个不同的数,通过如框图给出的一个算法输出一个整数a,则输出的数a=4的概率是( )
已知:a,b,c为集合A={1,2,3,4,5}中三个不同的数,通过如框图给出的一个算法输出一个整数a,则输出的数a=4的概率是( )| A. | $\frac{3}{8}$ | B. | $\frac{3}{20}$ | C. | $\frac{3}{10}$ | D. | $\frac{1}{2}$ |
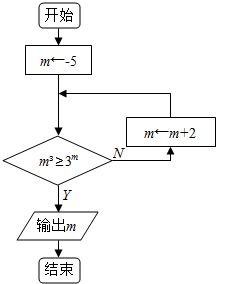
 根据如图所示的伪代码,如果输入x的值为0,则输出结果y为5.
根据如图所示的伪代码,如果输入x的值为0,则输出结果y为5.