题目内容
对抛物线x2=-4y,下列描述正确的是( )
A、开口向下,焦点为(0,-
| ||
| B、开口向下,焦点为(0,-1) | ||
C、开口向左,焦点为(-
| ||
| D、开口向左,焦点为(-1,0) |
分析:根据平方非负的性质得到抛物线上点的纵坐标为负数或零,所以抛物线开口向下.再由2p=4算出
=1,可得抛物线的焦点坐标,从而得到本题答案.
| p |
| 2 |
解答:解:∵抛物线方程为x2=-4y,∴由x2=-4y≥0,得y≤0.
即抛物线上点的纵坐标为负数或零,因此抛物线分布在三四象限,可得它的开口向下;
又∵2p=4,得
=1,∴抛物线的焦点坐标为(0,-1).
综上所述,抛物线x2=-4y开口向下且焦点为(0,-1).
故选:B
即抛物线上点的纵坐标为负数或零,因此抛物线分布在三四象限,可得它的开口向下;
又∵2p=4,得
| p |
| 2 |
综上所述,抛物线x2=-4y开口向下且焦点为(0,-1).
故选:B
点评:本题给出抛物线的标准方程,求它的开口方向与焦点坐标.着重考查了抛物线的标准方程及基本概念等知识,属于基础题.

练习册系列答案
相关题目
对抛物线x2=4y,下列描述正确的是( )
| A、开口向上,焦点为(0,1) | ||
B、开口向上,焦点为(0,
| ||
| C、开口向右,焦点为(1,0) | ||
D、开口向右,焦点为(
|
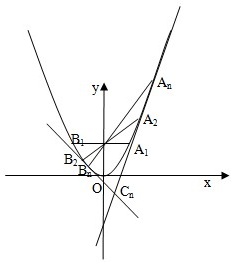 如图,对每个正整数n,An(xn,yn)是抛物线x2=4y上的点,过焦点F的直线FAn交抛物线于另一点Bn(sn,tn).
如图,对每个正整数n,An(xn,yn)是抛物线x2=4y上的点,过焦点F的直线FAn交抛物线于另一点Bn(sn,tn).