题目内容
设奇函数f（x）的定义域为实数集R，且满足f（x+1）=f（x-1），当x∈[0，1）时，f（x）=2x-1．则f(0)+f(
)+f(1)+f(
)+f(2)+f(
)的值为（ ）
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
A．
| B．
| C．0 | D．1-
|
∵f（x+1）=f（x-1），
∴f（x+2）=f（x）则f（x）是周期为2的周期函数
∵f（1）=f（-1）=-f（1）
∴f（1）=0
f(0)+f(
)+f(1)+f(
)+f(2)+f(
)=f（0）+f（
）+f（1）-f（
）+f（0）+f（
）
=0+
-1=
-1
故选B．
∴f（x+2）=f（x）则f（x）是周期为2的周期函数
∵f（1）=f（-1）=-f（1）
∴f（1）=0
f(0)+f(
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=0+
| 2 |
| 2 |
故选B．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
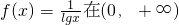是减函数；
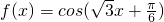，则f（x）+f'（x）是奇函数；
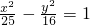的一个焦点到渐近线的距离是5；
是减函数；
，则f（x）+f'（x）是奇函数；
的一个焦点到渐近线的距离是5；