题目内容
已知定义在[1,+∞)上的函数f(x)=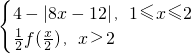 ,则
,则
- A.函数f(x)的值域为[1,4]
- B.关于x的方程f(x)-
 =0(n∈N*)有2n+4个不相等的实数根
=0(n∈N*)有2n+4个不相等的实数根 - C.当x∈[2n-1,2n](n∈N*)时,函数f(x)的图象与x轴围成的面积为2
- D.存在实数x0,使得不等式x0f(x0)>6成立
C
分析:分类讨论:①当1≤x≤ 时,f(x)=8x-8,;当
时,f(x)=8x-8,;当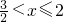 时,f(x)=16-8x;②当2<x≤3时,则
时,f(x)=16-8x;②当2<x≤3时,则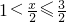 ,此时f(x)=
,此时f(x)=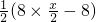 =
=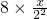 -4=2x-4;
-4=2x-4;
当3<x≤4时,则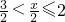 ,此时f(x)=
,此时f(x)=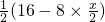 =8-
=8-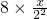 ;依此类推:当2n-1≤x≤3•2n-2时,f(x)=
;依此类推:当2n-1≤x≤3•2n-2时,f(x)= =25-2n(x-2n-1),
=25-2n(x-2n-1),
此时,0≤f(x)≤23-n;当3•2n-2<x≤2n时,f(x)=-25-2n(x-2n),此时,0≤f(x)≤23-n.据此即可判断答案.
解答:①当1≤x≤ 时,f(x)=8x-8,此时,0≤f(x)≤4;当
时,f(x)=8x-8,此时,0≤f(x)≤4;当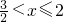 时,f(x)=16-8x,此时,0≤f(x)<4;
时,f(x)=16-8x,此时,0≤f(x)<4;
②当2<x≤3时,则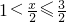 ,此时f(x)=
,此时f(x)=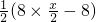 =
=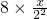 -4=2x-4,此时,0≤f(x)≤2;
-4=2x-4,此时,0≤f(x)≤2;
当3<x≤4时,则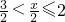 ,此时f(x)=
,此时f(x)=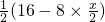 =8-
=8-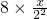 ,此时,0≤f(x)<2;
,此时,0≤f(x)<2;
…,
依此类推:当2n-1≤x≤3•2n-2时,f(x)= =25-2n(x-2n-1),
=25-2n(x-2n-1),
此时,0≤f(x)≤23-n;当3•2n-2<x≤2n时,f(x)=-25-2n(x-2n),此时,0≤f(x)≤23-n.
据此可得:函数f(x)的值域为[0,4],故A不正确;当n=1时, ,有且仅有7个不等实数根,不是2×1+4=6个不等实数根,故B不正确;当x∈[2n-1,2n](n∈N*)时,函数f(x)的图象与x轴围成的面积S=
,有且仅有7个不等实数根,不是2×1+4=6个不等实数根,故B不正确;当x∈[2n-1,2n](n∈N*)时,函数f(x)的图象与x轴围成的面积S=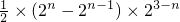 =2,故C正确;xf(x)>6?
=2,故C正确;xf(x)>6?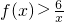 ,由f(x)的图象可得到:当x∈[2n-1,2n](n∈N*)时,
,由f(x)的图象可得到:当x∈[2n-1,2n](n∈N*)时,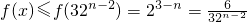 可得:
可得: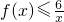 ,故D不正确.
,故D不正确.
综上可知:只有C正确.
故选C.
点评:本题综合考查了分类讨论思想方法、直线方程、函数的单调性、函数的交点与方程的根、如何否定一个命题等基础知识与基本技能,考查了数形结合的方法与能力、类比推理能力和计算能力.
分析:分类讨论:①当1≤x≤
 时,f(x)=8x-8,;当
时,f(x)=8x-8,;当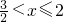 时,f(x)=16-8x;②当2<x≤3时,则
时,f(x)=16-8x;②当2<x≤3时,则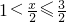 ,此时f(x)=
,此时f(x)=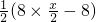 =
=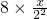 -4=2x-4;
-4=2x-4;当3<x≤4时,则
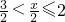 ,此时f(x)=
,此时f(x)=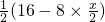 =8-
=8-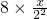 ;依此类推:当2n-1≤x≤3•2n-2时,f(x)=
;依此类推:当2n-1≤x≤3•2n-2时,f(x)= =25-2n(x-2n-1),
=25-2n(x-2n-1),此时,0≤f(x)≤23-n;当3•2n-2<x≤2n时,f(x)=-25-2n(x-2n),此时,0≤f(x)≤23-n.据此即可判断答案.
解答:①当1≤x≤
 时,f(x)=8x-8,此时,0≤f(x)≤4;当
时,f(x)=8x-8,此时,0≤f(x)≤4;当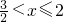 时,f(x)=16-8x,此时,0≤f(x)<4;
时,f(x)=16-8x,此时,0≤f(x)<4;
②当2<x≤3时,则
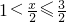 ,此时f(x)=
,此时f(x)=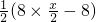 =
=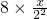 -4=2x-4,此时,0≤f(x)≤2;
-4=2x-4,此时,0≤f(x)≤2;当3<x≤4时,则
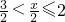 ,此时f(x)=
,此时f(x)=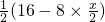 =8-
=8-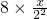 ,此时,0≤f(x)<2;
,此时,0≤f(x)<2;…,
依此类推:当2n-1≤x≤3•2n-2时,f(x)=
 =25-2n(x-2n-1),
=25-2n(x-2n-1),此时,0≤f(x)≤23-n;当3•2n-2<x≤2n时,f(x)=-25-2n(x-2n),此时,0≤f(x)≤23-n.
据此可得:函数f(x)的值域为[0,4],故A不正确;当n=1时,
 ,有且仅有7个不等实数根,不是2×1+4=6个不等实数根,故B不正确;当x∈[2n-1,2n](n∈N*)时,函数f(x)的图象与x轴围成的面积S=
,有且仅有7个不等实数根,不是2×1+4=6个不等实数根,故B不正确;当x∈[2n-1,2n](n∈N*)时,函数f(x)的图象与x轴围成的面积S=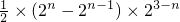 =2,故C正确;xf(x)>6?
=2,故C正确;xf(x)>6?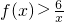 ,由f(x)的图象可得到:当x∈[2n-1,2n](n∈N*)时,
,由f(x)的图象可得到:当x∈[2n-1,2n](n∈N*)时,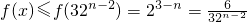 可得:
可得: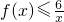 ,故D不正确.
,故D不正确.综上可知:只有C正确.
故选C.
点评:本题综合考查了分类讨论思想方法、直线方程、函数的单调性、函数的交点与方程的根、如何否定一个命题等基础知识与基本技能,考查了数形结合的方法与能力、类比推理能力和计算能力.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
已知定义在[1,8]上的函数 f(x)=
则下列结论中,错误的是( )
|
| A、f(6)=1 |
| B、函数f(x)的值域为[0,4] |
| C、将函数f(x)的极值由大到小排列得到数列{an},n∈N*,则{an}为等比数列 |
| D、对任意的x∈[1,8],不等式xf(x)≤6恒成立 |