题目内容
下列命题中,真命题的是( )A.
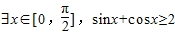
B.
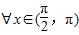 ,tanx>sin
,tanx>sinC.?x∈R,x2+x=-1
D.?x∈R,x2+2x>4x-3
【答案】分析:对于A:由于sinx+cosx=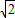 sin(x+
sin(x+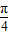 )
)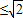 ,即可进行判断;对于B:当
,即可进行判断;对于B:当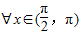 ,tanx<0,sinx>0.从而得出它们的大小关系;对于C:由于方程x2+x=-1的△<0,故此方程无实数解;对于D:先作差x2+2x-(4x-3)=x2-2x+3=(x-1)2+2≥0,再进行判断即可.
,tanx<0,sinx>0.从而得出它们的大小关系;对于C:由于方程x2+x=-1的△<0,故此方程无实数解;对于D:先作差x2+2x-(4x-3)=x2-2x+3=(x-1)2+2≥0,再进行判断即可.
解答:解:由于sinx+cosx=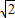 sin(x+
sin(x+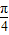 )
)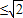 ,故
,故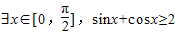 是假命题,A错;
是假命题,A错;
当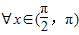 ,tanx<0,sinx>0.故
,tanx<0,sinx>0.故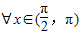 ,tanx>sinx是假命题,B错;
,tanx>sinx是假命题,B错;
由于方程x2+x=-1的△<0,故此方程无实数解,故C错;
由于x2+2x-(4x-3)=x2-2x+3=(x-1)2+2≥0.∴x2+2x>4x-3,故D正确.
故选D.
点评:本小题主要考查全称命题、特称命题、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.
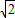 sin(x+
sin(x+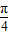 )
)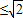 ,即可进行判断;对于B:当
,即可进行判断;对于B:当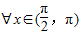 ,tanx<0,sinx>0.从而得出它们的大小关系;对于C:由于方程x2+x=-1的△<0,故此方程无实数解;对于D:先作差x2+2x-(4x-3)=x2-2x+3=(x-1)2+2≥0,再进行判断即可.
,tanx<0,sinx>0.从而得出它们的大小关系;对于C:由于方程x2+x=-1的△<0,故此方程无实数解;对于D:先作差x2+2x-(4x-3)=x2-2x+3=(x-1)2+2≥0,再进行判断即可.解答:解:由于sinx+cosx=
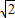 sin(x+
sin(x+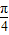 )
)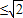 ,故
,故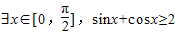 是假命题,A错;
是假命题,A错;当
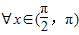 ,tanx<0,sinx>0.故
,tanx<0,sinx>0.故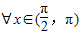 ,tanx>sinx是假命题,B错;
,tanx>sinx是假命题,B错;由于方程x2+x=-1的△<0,故此方程无实数解,故C错;
由于x2+2x-(4x-3)=x2-2x+3=(x-1)2+2≥0.∴x2+2x>4x-3,故D正确.
故选D.
点评:本小题主要考查全称命题、特称命题、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

练习册系列答案
相关题目
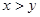 ,则
,则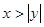 ”的逆命题
”的逆命题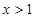 ,则
,则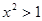 ”的否命题
”的否命题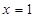 ,则
,则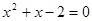 ”的否命题
”的否命题 ,则
,则