题目内容
 如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过C点.已知AB=3米,AD=2米.
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过C点.已知AB=3米,AD=2米.
(I)设AN=x(单位:米),要使花坛AMPN的面积大于32平方米,求x的取值范围;
(II)若x∈[3,4)(单位:米),则当AM,AN的长度分别是多少时,花坛AMPN的面积最大?并求出最大面积.
解:由于 ,则AM=
,则AM=
故SAMPN=AN•AM= (4分)
(4分)
(1)由SAMPN>32得 >32,
>32,
因为x>2,所以3x2-32x+64>0,即(3x-8)(x-8)>0
从而
即AN长的取值范围是 (8分)
(8分)
(2)令y= ,则y′=
,则y′= (10分)
(10分)
因为当x∈[3,4)时,y′<0,所以函数y= 在[3,4)上为单调递减函数,
在[3,4)上为单调递减函数,
从而当x=3时y= 取得最大值,即花坛AMPN的面积最大27平方米,
取得最大值,即花坛AMPN的面积最大27平方米,
此时AN=3米,AM=9米
分析:先由相似性表示AM,建立四边形AMPN的面积模型,(I)解关于x的不等式;
(II)先对面积函数模型求导,用导数法求最值.
点评:本题主要考查用相似性构建边的关系,建立平面图形面积函数模型及导数法解模求最值的能力.
 ,则AM=
,则AM=
故SAMPN=AN•AM=
 (4分)
(4分)(1)由SAMPN>32得
 >32,
>32,因为x>2,所以3x2-32x+64>0,即(3x-8)(x-8)>0
从而

即AN长的取值范围是
 (8分)
(8分)(2)令y=
 ,则y′=
,则y′= (10分)
(10分)因为当x∈[3,4)时,y′<0,所以函数y=
 在[3,4)上为单调递减函数,
在[3,4)上为单调递减函数,从而当x=3时y=
 取得最大值,即花坛AMPN的面积最大27平方米,
取得最大值,即花坛AMPN的面积最大27平方米,此时AN=3米,AM=9米
分析:先由相似性表示AM,建立四边形AMPN的面积模型,(I)解关于x的不等式;
(II)先对面积函数模型求导,用导数法求最值.
点评:本题主要考查用相似性构建边的关系,建立平面图形面积函数模型及导数法解模求最值的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
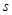 平方米,矩形一边的长为
平方米,矩形一边的长为 米(如图所示)
米(如图所示)
 平方米,矩形一边的长为
平方米,矩形一边的长为 米(如图所示)
米(如图所示)