题目内容
已知函数f（x）=
(x≠0). (1)若f(x)=x且x∈R,则称x为f(x)的实不动点.求f(x)的实不动点；
(2)在数列{an}中，a1=2,an+1=f(an),求数列{an}的通项公式.
解：(1)∵f(x)=x,∴
∴(x+1)4+(x-1)4=x·(x+1)4-x·(x-1)4.
∴(x+1)(x-1)[- (x+1)3+(x-1)3]=0.
∴(x+1)(x-1)(3x2+1)=0.
∴x=1或x=-1,
即f(x)的实不动点为x=1或x=-1.
(2)∵an+1=f(an),∴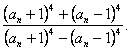
∴an·(an+1)4-an·(an-1)4=(an+1)4+(an-1)4.
∴(an+1)4·(an+1-1)=(an-1)4(an+1+1).
∴
=(
)4.
设bn=
,则上式为bn+1=bn4.
∵a1=2,∴b1=
=3, b2=b14=34,b3=b24=316,b4=b34=364…，猜想bn＝
证明如下：
① 当n=1时，有b1=3,符合.
② 假设当 n=k时，命题成立，即bk=
.
则当n=k时，bk＋1＝bk4=(
)4=3
也成立.
综合①②知bn=
成立.∴
＝
.∴
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
已知函数f（x）=x2-bx的图象在点A（1，f（1））处的切线l与直线3x-y+2=0平行，若数列{
}的前n项和为Sn，则S2010的值为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|