题目内容
对定义在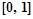 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数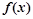 称为H函数.
称为H函数.
① 对任意的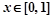 ,总有
,总有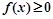 ;
;
② 当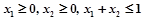 时,总有
时,总有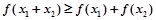 成立.
成立.
已知函数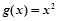 与
与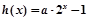 是定义在
是定义在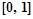 上的函数.
上的函数.
(1)试问函数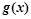 是否为H函数?并说明理由;
是否为H函数?并说明理由;
(2)若函数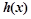 是H函数,求实数a的值;
是H函数,求实数a的值;
(3)在(2)的条件下,若方程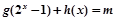 有解,求实数m的取值范围.
有解,求实数m的取值范围.
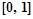 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数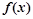 称为H函数.
称为H函数.① 对任意的
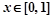 ,总有
,总有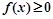 ;
;② 当
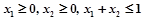 时,总有
时,总有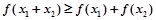 成立.
成立.已知函数
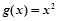 与
与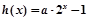 是定义在
是定义在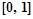 上的函数.
上的函数.(1)试问函数
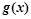 是否为H函数?并说明理由;
是否为H函数?并说明理由;(2)若函数
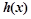 是H函数,求实数a的值;
是H函数,求实数a的值;(3)在(2)的条件下,若方程
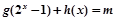 有解,求实数m的取值范围.
有解,求实数m的取值范围. 解:(1)函数 为
为 函数;
函数;
(2) (3)
(3) 时,方程有解
时,方程有解
 为
为 函数;
函数; (2)
 (3)
(3) 时,方程有解
时,方程有解本题考查新定义,考查利用新定义求参数的取值,考查换元法,考查配方法求函数的值域,解题的关键是正确理解新定义.
(1)根据G函数的定义,验证G函数的两个条件,即可判断;
(2)根据因为函数h(x)是G函数,利用G函数的两个条件,即可求得实数a的值;
(3)根据(2)知a=1,原方程可以化为4x-2x=m,再利用换元法,即可求实数m的取值范围
(1)根据G函数的定义,验证G函数的两个条件,即可判断;
(2)根据因为函数h(x)是G函数,利用G函数的两个条件,即可求得实数a的值;
(3)根据(2)知a=1,原方程可以化为4x-2x=m,再利用换元法,即可求实数m的取值范围

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 ,
, .
. ;
; ,并画出其图象;
,并画出其图象; 的解.
的解.
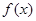 的定义域为
的定义域为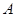 ,若
,若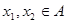 且
且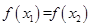 时总有
时总有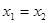 ,则称
,则称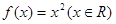 是单函数;
是单函数;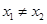 ,则
,则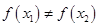 ;
;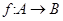 为单函数,则对于任意
为单函数,则对于任意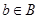 ,
,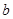 对应;
对应; ,满足
,满足 ,且
,且 ,
, .则
.则
 =.( )
=.( ) 的图象为( )
的图象为( )
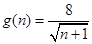 (
(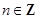 且n≥0),若产品销售价保持不变,第n次投入后的年利润为
且n≥0),若产品销售价保持不变,第n次投入后的年利润为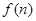 万元.
万元.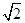 ,+∞)
,+∞)  ,则
,则 ______
______