题目内容
如图,从边长为a的正三角形的顶点,在各边上截取长度为x的线段,以这些线段为边作成有两个直角的四边形,这样的四边形有三个,把三个四边形剪掉,用剩下的部分折成一个底为正三角形的无盖柱形容器.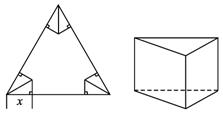
(1)求这个容器的容积V(x);
(2)求使V(x)为最大时的x的值及V(x)的最大值.
解:(1)柱形的高为![]() x,底面边长为(a-2x),所以底面积S=
x,底面边长为(a-2x),所以底面积S=![]() (a-2x)2sin60°=
(a-2x)2sin60°=![]() (a-2x)2.
(a-2x)2.
所以容积V(x)=![]() (a-2x)2×
(a-2x)2×![]() x=
x=![]() (0<x<
(0<x<![]() )?
)?
(2)V′(x)=![]() ,
,
令V′(x)=0,即12x2-8ax+a2=0.解得x1=![]() ,x2=
,x2=![]() (不合题意,舍去).因为V(x)在(0,
(不合题意,舍去).因为V(x)在(0,![]() )上只有一个极值,所以它是最大值,V(x)max=V(
)上只有一个极值,所以它是最大值,V(x)max=V(![]() )=
)=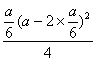 =
=![]() .所以使V(x)为最大值时的x的值是
.所以使V(x)为最大值时的x的值是![]() ,V(x)的最大值是
,V(x)的最大值是![]() .
.

练习册系列答案
相关题目
 如图,已知正三棱锥P-ABC的侧棱长为
如图,已知正三棱锥P-ABC的侧棱长为
 如图,已知正三棱锥P-ABC的侧棱长为
如图,已知正三棱锥P-ABC的侧棱长为 ,底面边长为
,底面边长为 ,高为2,
,高为2,



 ,高为2,一只蚂蚁要从顶点A沿三棱柱的表面爬到顶点C′,若侧面AA′C′C紧贴墙面(不能通行),则爬行的最短路程是
,高为2,一只蚂蚁要从顶点A沿三棱柱的表面爬到顶点C′,若侧面AA′C′C紧贴墙面(不能通行),则爬行的最短路程是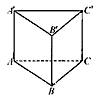


 +
+