题目内容
已知数列![]() 的前
的前![]() 项和
项和![]() 满足
满足![]() ,且
,且![]()
![]()
(1)求k的值;
(2)求![]() ;
;
(3)是否存在正整数![]() ,使
,使![]() 成立?若存在,求出这样的正整数;若不存在,说明理由.
成立?若存在,求出这样的正整数;若不存在,说明理由.
(1)![]() ;(2)
;(2) ;(3)存在正整数
;(3)存在正整数![]()
解析:
(1) ![]()
又![]() ,∴
,∴![]()
![]()
(2) 由 (1) 知 ![]() ①
①
当![]() 时,
时,![]() ②
②
①-②,得![]()
又![]() ,易见
,易见![]()
于是![]() 是等比数列,公比为
是等比数列,公比为![]() ,所以
,所以
(3) 不等式![]() ,即
,即 .;整理得
.;整理得![]()
假设存在正整数![]() 使得上面的不等式成立,由于2n为偶数,
使得上面的不等式成立,由于2n为偶数,![]() 为整数,
为整数,
则只能是![]()
![]()
因此,存在正整数![]()

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 的前
的前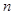 项和
项和 满足:
满足: ,且
,且 ,那么
,那么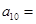 ( )
( ) 的前
的前 项和
项和 满足
满足 ,等差数列
,等差数列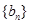 满足
满足 ,
, 。
。 ,数列
,数列 的前
的前 ,问
,问 >
> 的最小正整数
的最小正整数