题目内容
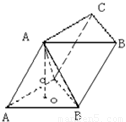
如图是各棱长均为a的斜三棱柱ABC-A1B1C1，∠A1AC=∠A1AB=60°．求证：三棱锥A1-ABC是正四面体．分析：欲证明三棱锥A1-ABC是正四面体，只须证明其四个面都是正三角形即可．
解答：证明：∵如图是各棱长均为a的斜三棱柱ABC-A1B1C1，∠A1AC=∠A1AB=60°．
∴△ABC，△A1AB，△A1AC都是正三角形，从而△A1BC也是正三角形，
即三棱锥A1-ABC的四个面都是正三角形，
∴三棱锥A1-ABC是正四面体．
∴△ABC，△A1AB，△A1AC都是正三角形，从而△A1BC也是正三角形，
即三棱锥A1-ABC的四个面都是正三角形，
∴三棱锥A1-ABC是正四面体．
点评：本题考查棱锥的结构特征，等边三角形的性质，属于基础题．
练习册系列答案
状元坊全程突破导练测系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
如图，P-ABC是底面边长为1的正三棱锥，D、E、F分别为棱长PA、PB、PC上的点，截面DEF∥底面ABC，且棱台DEF-ABC与棱锥P-ABC的棱长和相等．（棱长和是指多面体中所有棱的长度之和）
