题目内容
已知函数f(x)=(cosωx+sinωx)(cosωx-sinωx)+2 sinωx•cosωx+t(ω>0),若f(x)的图象上相邻两条对称轴之间的距离为
sinωx•cosωx+t(ω>0),若f(x)的图象上相邻两条对称轴之间的距离为 ,且当x∈[0,π]时,函数f(x)的最大值为1.
,且当x∈[0,π]时,函数f(x)的最大值为1.
(1)求函数f(x)的表达式;(2)在△ABC中,若f(C)=1,且2sin2B=cosB+cos(A-C),求sinA的值.
解:(1)
=
= (4分)
(4分)
由题意有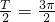
∴ ∴
∴ (5分)
(5分)
∵0≤x≤π∴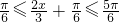
∴f(x)max=2+t=1
∴t=-1(16分)
∴ (7分)
(7分)
(2)∵
∴
又 0<C<π∴
∴ ∴
∴ (9分)
(9分)
∴
∴原方程可化为2cos2A=sinA+sinA
即sin2A+sinA-1=0
解得
∵0<sinA<1
∴ (12分)
(12分)
分析:(1)先根据二倍角公式对函数解析式进行整理得到f(x)= ;再结合图象上相邻两条对称轴之间的距离为
;再结合图象上相邻两条对称轴之间的距离为 ,且当x∈[0,π]时,函数f(x)的最大值为1求出ω,t即可求出函数f(x)的表达式;
,且当x∈[0,π]时,函数f(x)的最大值为1求出ω,t即可求出函数f(x)的表达式;
(2)先根据f(C)=1求出角C;再结合2sin2B=cosB+cos(A-C),把B用A表示出来,即可求出sinA的值.
点评:本题考查的知识点是由函数y=Asin(ωx+∅)的图象确定函数的解析式,解决这类问题的关键在于根据函数的图象分析出函数的最大值,最小值,周期,向左平移量,特殊点.

=

=
 (4分)
(4分)由题意有
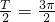
∴
 ∴
∴ (5分)
(5分)∵0≤x≤π∴
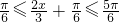
∴f(x)max=2+t=1
∴t=-1(16分)
∴
 (7分)
(7分)(2)∵

∴

又 0<C<π∴

∴
 ∴
∴ (9分)
(9分)∴

∴原方程可化为2cos2A=sinA+sinA
即sin2A+sinA-1=0
解得

∵0<sinA<1
∴
 (12分)
(12分)分析:(1)先根据二倍角公式对函数解析式进行整理得到f(x)=
 ;再结合图象上相邻两条对称轴之间的距离为
;再结合图象上相邻两条对称轴之间的距离为 ,且当x∈[0,π]时,函数f(x)的最大值为1求出ω,t即可求出函数f(x)的表达式;
,且当x∈[0,π]时,函数f(x)的最大值为1求出ω,t即可求出函数f(x)的表达式;(2)先根据f(C)=1求出角C;再结合2sin2B=cosB+cos(A-C),把B用A表示出来,即可求出sinA的值.
点评:本题考查的知识点是由函数y=Asin(ωx+∅)的图象确定函数的解析式,解决这类问题的关键在于根据函数的图象分析出函数的最大值,最小值,周期,向左平移量,特殊点.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|