题目内容
如图2-5-8,已知PA为⊙O的切线,PBD为⊙O的割线,交⊙O于B、D两点,C为AB中点,PC的延长线交AD于E.求证:PA2∶PB2=DE∶EA.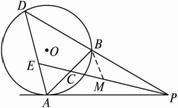
图2-5-8
思路解析:此题涉及平方比问题,我们应设法化去平方比PA2∶PB2,由于PA2=PB·PD,故可以用这一结论直接化去平方比.
证明:过B作BM∥AD,交PC于点M,?
∵PA2=PB·PD,∴
=
=
.?
∵C为AB中点,∴BC =AC.?
∵BM∥AE,∴AE =BM,且
=
.?
∴
=
.∴
=
.
练习册系列答案
相关题目
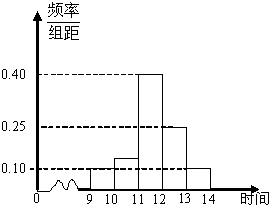某商场在国庆黄金周的促销活动中，对10月2日9时到14时的销售额进行统计，其频率分布直方图如图所示，已知9时至10时的销售额为2.5万元，则11时到12时的销售额为（ ）| A、6万元 | B、8万元 | C、10万元 | D、12万元 |
28、为了了解噪声污染的情况，某市环保局抽样调查了80个测量点的噪声声级（单位：分贝），并进行整理后分成五组，绘制出频率分布直方图，如图所示．已知从左至右前四组的频率分别是0.15，0.25，0.3，0.2，且噪声声级高于69.5分贝就会影响工作和生活，那么影响到工作和生活而需对附近区域进行治理的测量点有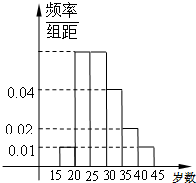
某单位组织群众性登山健身活动，招募了N名师生志愿者，将所有志愿者现按年龄情况分为15-20，20-25，25-30，30-35，35-40，40-45等六个层次，其频率分布直方图如图所示：已知30-35之间的志愿者共8人．