题目内容
已知i为虚数单位，集合A={n∈N*|in=-1}，则集合A中的最小元素为（ ）
分析：利用虚数单位i 的幂运算性质，有 n=4k+2，k∈z，再由n∈N*，求得集合A中的最小元素．
解答：解：i为虚数单位，集合A={n∈N*|in=-1}，则 n=4k+2，k∈z，则集合A中的最小元素为n=2，
故选 A．
故选 A．
点评：本题考查虚数单位i 的幂运算性质的应用，凡是满足in=-1的整数n，一定可以写成 n=4k+2，k∈z的形式．
练习册系列答案
相关题目
是实数，则a=1；
；
；
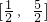在定义城内是减函数，则“p∧q”为真，“p∧q”为假，“￢p”为真．
是实数，则a=1；
；
；
在定义城内是减函数，则“p∧q”为真，“p∧q”为假，“￢p”为真．