题目内容
在△ABC中,若 ,则tanA:tanB:tanC= ,tanA= .
,则tanA:tanB:tanC= ,tanA= .
【答案】分析:先根据平面向量的数量积运算,把 ,
, ,
, 变形,则
变形,则 ,就可化简为关于tanA,tanB,tanC的等式,进而求出tanA:tanB:tanC,根据前面求出的tanA:tanB:tanC,把tanB,tanC均用tanA表示,再利用三角形内角和定理,和两角和的正切公式,得到含tanA的等式,解出tanA.
,就可化简为关于tanA,tanB,tanC的等式,进而求出tanA:tanB:tanC,根据前面求出的tanA:tanB:tanC,把tanB,tanC均用tanA表示,再利用三角形内角和定理,和两角和的正切公式,得到含tanA的等式,解出tanA.
解答:解;根据平面向量的数量积运算, =AB•BCcosB,
=AB•BCcosB, =BC•CAcosC,
=BC•CAcosC, =CA•ABcosA
=CA•ABcosA
∵ ,∴
,∴ =
= =
=
根据正弦定理,得, =
= =
= ,
,
化简得, ,
, ,∴tanA:tanB:tanC=6:2:3
,∴tanA:tanB:tanC=6:2:3
∴tanB= tanA,tanC=
tanA,tanC= tanA,
tanA,
在△ABC中,A=π-B-C,tanA=-tan(B+C)=- =-
=- ,∴tanA=±
,∴tanA=± ,
,
∵tanA:tanB:tanC=6:2:3,∴tanA=- 不成立,∴tanA=
不成立,∴tanA= ,
,
故答案为=6:2:3;
点评:本题考查了平面向量的数量积运算,三角形内角和定理,正弦定理,两角和的正切公式,综合性较强,做题时应认真分析.
 ,
, ,
, 变形,则
变形,则 ,就可化简为关于tanA,tanB,tanC的等式,进而求出tanA:tanB:tanC,根据前面求出的tanA:tanB:tanC,把tanB,tanC均用tanA表示,再利用三角形内角和定理,和两角和的正切公式,得到含tanA的等式,解出tanA.
,就可化简为关于tanA,tanB,tanC的等式,进而求出tanA:tanB:tanC,根据前面求出的tanA:tanB:tanC,把tanB,tanC均用tanA表示,再利用三角形内角和定理,和两角和的正切公式,得到含tanA的等式,解出tanA.解答:解;根据平面向量的数量积运算,
 =AB•BCcosB,
=AB•BCcosB, =BC•CAcosC,
=BC•CAcosC, =CA•ABcosA
=CA•ABcosA∵
 ,∴
,∴ =
= =
=
根据正弦定理,得,
 =
= =
= ,
,化简得,
 ,
, ,∴tanA:tanB:tanC=6:2:3
,∴tanA:tanB:tanC=6:2:3∴tanB=
 tanA,tanC=
tanA,tanC= tanA,
tanA,在△ABC中,A=π-B-C,tanA=-tan(B+C)=-
 =-
=- ,∴tanA=±
,∴tanA=± ,
,∵tanA:tanB:tanC=6:2:3,∴tanA=-
 不成立,∴tanA=
不成立,∴tanA= ,
,故答案为=6:2:3;

点评:本题考查了平面向量的数量积运算,三角形内角和定理,正弦定理,两角和的正切公式,综合性较强,做题时应认真分析.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则B的值为( )
,则B的值为( )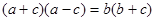 ,则∠A=( )
,则∠A=( ) B.
B. C.
C.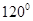 D.
D.
 ,则∠A=
,则∠A= 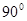 B.
B.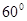 C.
C. D.
D.
 ,
, ,若
,若 ,
, ,则
,则 ()
()  A.
A. B.
B.
 D.
D.
 ,则其面积等于( )
,则其面积等于( ) B.
B. C.1
D.2
C.1
D.2