Question

如图，在正方形ABCD中，PB=BC，PB⊥平面ABCD，则PC与BD所成的角是（　　）

A．90°

B．45°

C．60°

D．30°

Answer 1

分析：取PA的中点E，连接AC，AC交BD于点G，连接EG，由三角形中位线定理，可得EG∥PC，把PC与BD所成的角转化为∠EGB或其补角，然后在三角形BEG中求出∠EGB即可．

解答：解：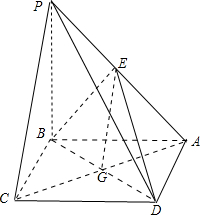
取PA的中点E，
如图，连接AC，AC交BD于点G，连接EG．
∵底面ABCD是正方形，∴G为AC的中点．
又E为PA的中点，∴EG∥PC．
∴∠EGB或其补角即为PC与BD所成的角
∵在正方形ABCD中，PB=BC，PB⊥平面ABCD，
∴PC=PA=BD
∵BG=

1

2

BD，EG=

1

2

PC，BE=

1

2

PA，
∴BG=EG=BE
∴∠EGB=60°．
故PC与BD所成的角为：60°．
故选C．

点评：本题主要考查异面直线及其所成的角．异面直线所成角的求法一般是通过平移转化为相交直线，然后在三角形中求解．