题目内容
如图,在四棱锥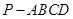 中,底面
中,底面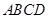 为直角梯形,且
为直角梯形,且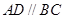 ,
, ,侧面
,侧面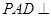 底面
底面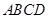 . 若
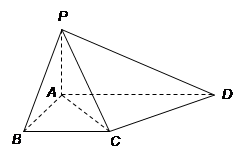
. 若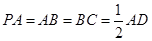 .
.
(Ⅰ)求证: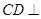 平面
平面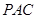 ;
;
(Ⅱ)侧棱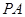 上是否存在点
上是否存在点 ,使得
,使得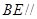 平面
平面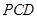 ?若存在,指出点
?若存在,指出点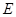 的位置并证明,若不存在,请说明理由;
的位置并证明,若不存在,请说明理由;
(Ⅲ)求二面角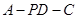 的余弦值.
的余弦值.
(1) 对于线面垂直的证明主要是根据线面垂直的判定定理,先通过线线垂直来得到证明。(2)
解析试题分析:解法一:
(Ⅰ)因为  ,所以
,所以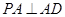 .
.
又因为侧面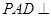 底面
底面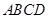 ,且侧面
,且侧面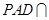 底面
底面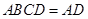 ,所以
,所以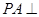 底面
底面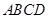 .而
.而 底面
底面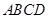 ,所以
,所以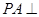
 . 2分
. 2分
在底面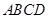 中,因为
中,因为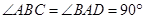 ,
,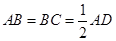 ,
,
所以 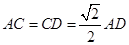 , 所以
, 所以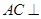
 .
.
又因为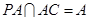 , 所以
, 所以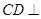 平面
平面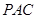 . 4分
. 4分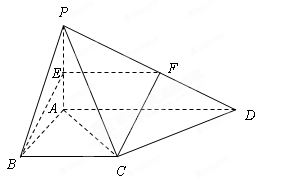
(Ⅱ)在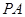 上存在中点
上存在中点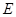 ,使得
,使得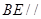 平面
平面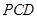 ,
,
证明如下:设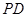 的中点是
的中点是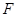 , 连结
, 连结 ,
,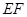 ,
,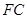 ,则
,则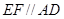 ,且
,且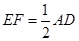 . 由已知
. 由已知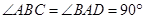 ,所以
,所以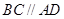 . 又
. 又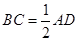 ,所以
,所以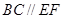 ,且
,且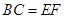 ,
,
所以四边形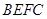 为平行四边形,所以
为平行四边形,所以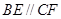 .
.
因为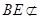 平面
平面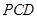 ,
,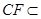 平面
平面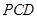 ,
,
所以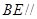 平面
平面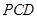 . 8分
. 8分
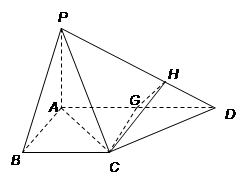
(Ⅲ)设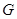 为
为 中点,连结
中点,连结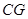 ,
,
则 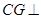
 .又因为平面
.又因为平面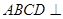 平面
平面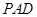 ,
,
所以 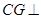 平面
平面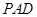 .过
.过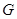 作
作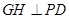 于
于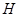 ,
,
连结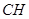 ,则
,则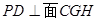 ,所以
,所以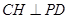
所以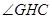 是二面角
是二面角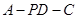 的平面角.
的平面角.
设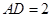 ,则
,则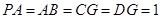 ,
, 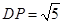 .在
.在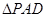 中,由相似三角形可得:
中,由相似三角形可得: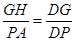 ,所以
,所以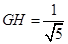 .所以
.所以 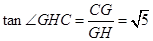 ,
,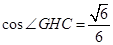 .即二面角
.即二面角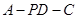 的余弦值为
的余弦值为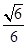 . 14分
. 14分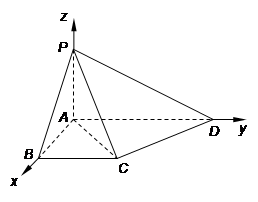

练习册系列答案
相关题目
 平面
平面 是正三角形,且
是正三角形,且 .
.
 是线段
是线段 的中点,求证:
的中点,求证: ∥平面
∥平面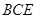 ;
;  与平面
与平面 所成角的余弦值.
所成角的余弦值.
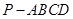 中,
中,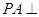 平面ABCD,底面ABCD是菱形,
平面ABCD,底面ABCD是菱形,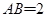 ,
,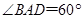 .
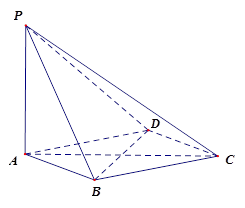
.
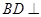 平面PAC;
平面PAC;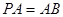 ,求PB与AC所成角的余弦值;
,求PB与AC所成角的余弦值;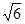 ,求证:平面PBC⊥平面PDC
,求证:平面PBC⊥平面PDC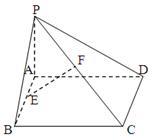
 与正三角形
与正三角形 所在的平面相互垂直,且
所在的平面相互垂直,且 、
、
 、
、 中点.
中点.
 ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 ;
;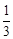 ,求AB的长.
,求AB的长.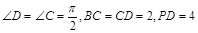 ,A为PD的中点,如下左图。将
,A为PD的中点,如下左图。将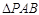 沿AB折到
沿AB折到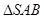 的位置,使
的位置,使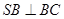 ,点E在SD上,且
,点E在SD上,且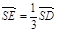 ,如下图。
,如下图。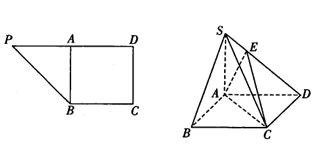
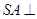 平面ABCD;
平面ABCD;