题目内容
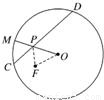
如图，一圆形纸片的圆心为O，F是圆内一定点，M是圆周上一动点，MF的垂直平分线CD交OM于P，则点P的轨迹是
- A.椭圆
- B.双曲线
- C.抛物线
- D.圆
A
分析：根据垂直平分线的性质可得|PM|=|PF|，可得|PO|+|PF|=|OM|＞|OF|，故点P的轨迹是以点O 和点F 为焦点的椭圆．
解答：根据垂直平分线的性质可得|PM|=|PF|，∴|PO|+|PF|=|OM|＞|OF|，
即点P到点O和点F的距离之和等于圆的半径|OM|，且|OM|＞|OF|，
根据椭圆的定义可得点P的轨迹是以点O和点F为焦点的椭圆，
故选A．
点评：本题考查椭圆的定义、线段的垂直平分线的性质，得到|PO|+|PF|=半径|OM|＞|OF|，是解题的关键．
分析：根据垂直平分线的性质可得|PM|=|PF|，可得|PO|+|PF|=|OM|＞|OF|，故点P的轨迹是以点O 和点F 为焦点的椭圆．
解答：根据垂直平分线的性质可得|PM|=|PF|，∴|PO|+|PF|=|OM|＞|OF|，
即点P到点O和点F的距离之和等于圆的半径|OM|，且|OM|＞|OF|，
根据椭圆的定义可得点P的轨迹是以点O和点F为焦点的椭圆，
故选A．
点评：本题考查椭圆的定义、线段的垂直平分线的性质，得到|PO|+|PF|=半径|OM|＞|OF|，是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
3、如图，一圆形纸片的圆心为O，F是圆内一定点，M是圆周上一动点，把纸片折叠使M与F重合，然后抹平纸片，折痕为CD，设CD与OM交于点P，则点P的轨迹是（ ）
如图，一圆形纸片的圆心为O，F是圆内一定点，M是圆周上一动点，MF的垂直平分线CD交OM于P，则点P的轨迹是（ ）
）
）