Question

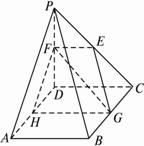
如图(1),在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分别是线段PC,PD,BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD〔如图(2)〕.

(1)求证:AP∥平面EFG;

(2)求二面角G-EF-D的大小;

(3)在线段PB上确定一点Q,使PC⊥平面ADQ,试给出证明.

Answer 1

证明：取AD的中点H，连HG，HF，?

∵E、F、G分别是线段PC、PD、BC的中点，?

∴EF∥DC,HG∥DC.?

∴HG∥EF，E、F、H、G四点共面.?

∴HF面EFHG.?

∵HF∥AP，AP面EFGH，?

∴AP∥面EFGH，即AP∥平面EFG.                                                                           

?

(2)解：∵PD⊥DC，EF∥DC，?

∴DF⊥EF.又平面PDC⊥平面ABCD，且HD⊥DC，?

∴HD⊥平面PDC，EF平面PDC,由三垂线定理得HF⊥EF.?

∴∠DFH就是二面角G-EF-D的平面角.                                                                 ?

在RT△HDF中，DF=PD=1，DH=AD=1，?

∴∠DFH=45°，即二面角GEFD的大小为45°.                                                       

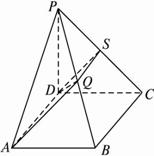
(3)证法一：当点Q是线段PB中点时，有PC⊥平面ADQ.?

证明如下:?

取PC中点S,连QS、DS,则有QS∥BC,?

又BC∥AD,?

∴QS∥AD.?

∴A、D、S、Q四点共面.?

∵PD=DC,S为PC中点,?

∴PC⊥DS.?

又∵PD⊥平面ABCD,AD⊥CD,??

∴AD⊥PC.又AD∩DS=D，?

∴PC⊥平面ADSQ，即PC⊥平面ADQ.                                                                        

?

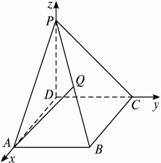
证法二：建立如图所示的空间直角坐标系.设Q是线段PB上的一点，?

令=λ(0＜λ＜1),?

∵PD=AD=2,?

∴P(0,0,2),A(2,0,0),B(2,2,0),C(0,2,0).?

∴=(-2,0,2),=(2,2,-2),=(0,2,-2).∴=(2λ,2λ,-2λ).?

∴=+=(-2+2λ,2λ,2-2λ).令·=0,

设2·2λ-2(2-2λ)=0，?

解得λ=.?

∴当λ=，即点Q是线段PB中点时，有AQ⊥PC.?

又∵PD⊥平面ABCD，AD⊥CD，?

∴AD⊥PC.?

∴当点E是线段PB中点时，有PC⊥平面ADQ.?