题目内容
一个袋中装有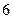 个形状大小完全相同的小球,球的编号分别为
个形状大小完全相同的小球,球的编号分别为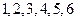 .
.
(Ⅰ)若从袋中每次随机抽取1个球,有放回的抽取2次,求取出的两个球编号之和为6的概率;
(Ⅱ)若从袋中每次随机抽取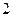 个球,有放回的抽取3次,求恰有
个球,有放回的抽取3次,求恰有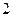 次抽到
次抽到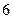 号球的概率;
号球的概率;
(Ⅲ)若一次从袋中随机抽取 个球,记球的最大编号为
个球,记球的最大编号为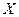 ,求随机变量
,求随机变量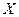 的分布列.
的分布列.
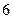 个形状大小完全相同的小球,球的编号分别为
个形状大小完全相同的小球,球的编号分别为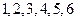 .
.(Ⅰ)若从袋中每次随机抽取1个球,有放回的抽取2次,求取出的两个球编号之和为6的概率;
(Ⅱ)若从袋中每次随机抽取
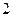 个球,有放回的抽取3次,求恰有
个球,有放回的抽取3次,求恰有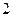 次抽到
次抽到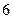 号球的概率;
号球的概率;(Ⅲ)若一次从袋中随机抽取
 个球,记球的最大编号为
个球,记球的最大编号为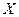 ,求随机变量
,求随机变量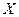 的分布列.
的分布列.(Ⅰ)

(Ⅱ)

(Ⅲ)
 |  |  |  | 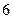 |
 |  |  |  |  |
解:(Ⅰ)设先后两次从袋中取出球的编号为 ,则两次取球的编号的一切可能结果
,则两次取球的编号的一切可能结果 有
有 种, ………………2分
种, ………………2分
其中和为6的结果有(1,5),(5,2),(2,4),(4,2),(3,3),共5种,则所求概率为 . ………………4分
. ………………4分
(Ⅱ)每次从袋中随机抽取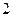 个球,抽到编号为
个球,抽到编号为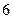 的球的概率
的球的概率 .……6分
.……6分
所以, 次抽取中,恰有
次抽取中,恰有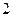 次抽到6号球的概率为
次抽到6号球的概率为
 . ………………8分
. ………………8分
(Ⅲ)随机变量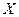 所有可能的取值为
所有可能的取值为 . ………………9分
. ………………9分
 ,
,
 ,
,
 ,
,
 . ………………12分
. ………………12分
所以,随机变量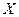 的分布列为:
的分布列为:
…13分
 ,则两次取球的编号的一切可能结果
,则两次取球的编号的一切可能结果 有
有 种, ………………2分
种, ………………2分其中和为6的结果有(1,5),(5,2),(2,4),(4,2),(3,3),共5种,则所求概率为
 . ………………4分
. ………………4分(Ⅱ)每次从袋中随机抽取
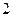 个球,抽到编号为
个球,抽到编号为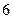 的球的概率
的球的概率 .……6分
.……6分所以,
 次抽取中,恰有
次抽取中,恰有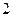 次抽到6号球的概率为
次抽到6号球的概率为 . ………………8分
. ………………8分(Ⅲ)随机变量
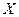 所有可能的取值为
所有可能的取值为 . ………………9分
. ………………9分 ,
, ,
, ,
, . ………………12分
. ………………12分所以,随机变量
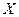 的分布列为:
的分布列为: |  |  |  | 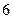 |
 |  |  |  |  |

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
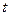 名学生在一次百米测试中,成绩全部介于13秒和18秒之间。将测试结果按如下方式分为五组:第一组[13,14);第二组[14,15);…;第五组[17,18],表是
名学生在一次百米测试中,成绩全部介于13秒和18秒之间。将测试结果按如下方式分为五组:第一组[13,14);第二组[14,15);…;第五组[17,18],表是 按上述分组方式得到的频率分布表。
按上述分组方式得到的频率分布表。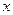
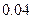
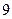
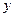
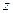

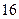
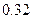
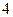
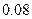
 的值;
的值; 百米测试成绩,求事件“
百米测试成绩,求事件“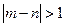 ”的
”的 概率.
概率. ,求抽奖者获奖的概率;
,求抽奖者获奖的概率; 表示获奖的人数,求
表示获奖的人数,求 的值.
的值. ,甲、乙、丙三人都做对的概率是
,甲、乙、丙三人都做对的概率是 ,甲、乙、丙全部做错的概率是
,甲、乙、丙全部做错的概率是 .
. 之和(单位:元),已知某顾客得到一次摸奖机会。
之和(单位:元),已知某顾客得到一次摸奖机会。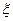 (元)为该顾客摸球停止时所得的奖金数,求
(元)为该顾客摸球停止时所得的奖金数,求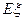 .
.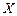 的概率分布列和数学期望.
的概率分布列和数学期望.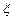 服从正态分布
服从正态分布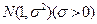 .若
.若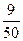 ;
;