题目内容
设函数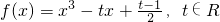 .
.
(I)试讨论函数f(x)在区间[0,1]上的单调性:
(II)求最小的实数h,使得对任意x∈[0,1]及任意实数t,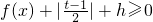 恒成立.
恒成立.
解:(1)∵函数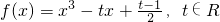 ,∴f′(x)=3x2-t.
,∴f′(x)=3x2-t.
1°若t≤0,则f′(x)≥0(不恒等于0)在[0,1]上恒成立,∴f(x)在[0,1]上单调递增;
2°若t≥3时,∵3x2≤3,∴f′(x)≤0在[0,1]上恒成立,∴f(x)在[0,1]上单调递减;
3°若0<t<3,则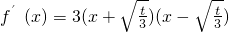 ,令f′(x)=0,解得
,令f′(x)=0,解得 ,
,
当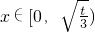 时,f′(x)<0,∴f(x)在
时,f′(x)<0,∴f(x)在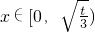 上单调递减;
上单调递减;
当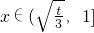 时,f′(x)>0,∴f(x)在
时,f′(x)>0,∴f(x)在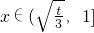 上单调递增.
上单调递增.
(2)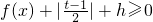 ?
? ,因此,只需求出当x∈[0,1],t∈R时,
,因此,只需求出当x∈[0,1],t∈R时,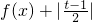 的最小值即可.
的最小值即可.
方法一:令g(x)=f(x)+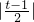 ,x∈[0,1],
,x∈[0,1],
而g′(x)=f′(x),由(1)的结论可知:
当t≤0或t≥3时,则g(x)在[0,1]上单调,故g(x)min=min{g(0),g(1)}=min{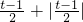 ,
,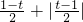 }=0.
}=0.
当0<t<3时,则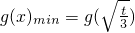 =-
=-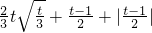 .
.
∴h(t)=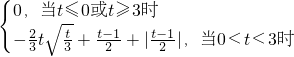 .
.
下面求当t∈R时,关于t的函数h(t)的最小值.
当t∈(0,1)时,h(t)=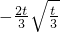 在(0,1)上单调递减;
在(0,1)上单调递减;
当1<t<3时,h(t)=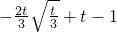 ,
,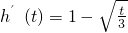 >0,∴h(t)在(1,3)上单调递增.又h(t)在t=1处连续,故h(t)在t∈(0,3)上的最小值是h(1)=-
>0,∴h(t)在(1,3)上单调递增.又h(t)在t=1处连续,故h(t)在t∈(0,3)上的最小值是h(1)=-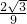 .
.
综上可知:当t∈[0,1]且t∈R时,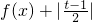 的最小值为
的最小值为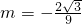 ,即得h的最小值为-m=
,即得h的最小值为-m=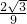 .
.
方法2:对于给定的x∈[0,1],求关于t的函数(t∈R),
g(t)=f(x)+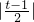 =-xt+
=-xt+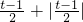 +x3=
+x3=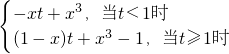 的最小值.
的最小值.
由于-x≤0,当t∈(-∞,1)时,g′(t)≤0;由于1-x≥0,故当t∈(1,+∞)时,g′(t)≥0.
考虑到g(t)在t=1处连续,∴g(t)的最小值h(x)=x3-x.
下面再求关于x的函数h(x)=x3-x在x∈[0,1]时的最小值.
h′(x)=3x2-1,令h′(x)=0,解得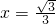 .
.
当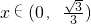 时,h′(x)<0,函数h(x)在此区间上单调递减;当
时,h′(x)<0,函数h(x)在此区间上单调递减;当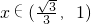 时,h′(x)>0,函数h(x)在此区间上单调递增.
时,h′(x)>0,函数h(x)在此区间上单调递增.
故h(x)的最小值为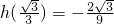 .
.
综上可得:当x∈(0,1)时,且t∈R.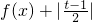 的最小值m=-
的最小值m=-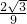 ,即得h的最小值为-m=
,即得h的最小值为-m=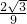 .
.
分析:(1)对t分类讨论,利用导数与单调性的关系即可得出;
(2)把问题正确等价转化,通过分类讨论,利用导数研究函数的单调性和最值,即可得出.
点评:熟练掌握分类讨论的思想方法、利用导数研究函数单调性、极值、最值、及把问题正确等价转化是解题的关键.
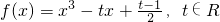 ,∴f′(x)=3x2-t.
,∴f′(x)=3x2-t.1°若t≤0,则f′(x)≥0(不恒等于0)在[0,1]上恒成立,∴f(x)在[0,1]上单调递增;
2°若t≥3时,∵3x2≤3,∴f′(x)≤0在[0,1]上恒成立,∴f(x)在[0,1]上单调递减;
3°若0<t<3,则
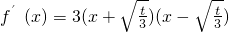 ,令f′(x)=0,解得
,令f′(x)=0,解得 ,
,当
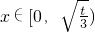 时,f′(x)<0,∴f(x)在
时,f′(x)<0,∴f(x)在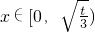 上单调递减;
上单调递减;当
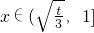 时,f′(x)>0,∴f(x)在
时,f′(x)>0,∴f(x)在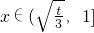 上单调递增.
上单调递增.(2)
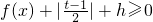 ?
? ,因此,只需求出当x∈[0,1],t∈R时,
,因此,只需求出当x∈[0,1],t∈R时,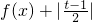 的最小值即可.
的最小值即可.方法一:令g(x)=f(x)+
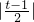 ,x∈[0,1],
,x∈[0,1],而g′(x)=f′(x),由(1)的结论可知:
当t≤0或t≥3时,则g(x)在[0,1]上单调,故g(x)min=min{g(0),g(1)}=min{
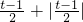 ,
,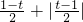 }=0.
}=0.当0<t<3时,则
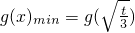 =-
=-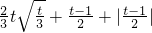 .
.∴h(t)=
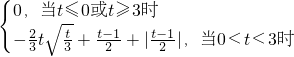 .
.下面求当t∈R时,关于t的函数h(t)的最小值.
当t∈(0,1)时,h(t)=
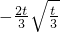 在(0,1)上单调递减;
在(0,1)上单调递减;当1<t<3时,h(t)=
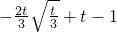 ,
,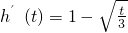 >0,∴h(t)在(1,3)上单调递增.又h(t)在t=1处连续,故h(t)在t∈(0,3)上的最小值是h(1)=-
>0,∴h(t)在(1,3)上单调递增.又h(t)在t=1处连续,故h(t)在t∈(0,3)上的最小值是h(1)=-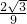 .
.综上可知:当t∈[0,1]且t∈R时,
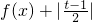 的最小值为
的最小值为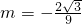 ,即得h的最小值为-m=
,即得h的最小值为-m=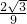 .
.方法2:对于给定的x∈[0,1],求关于t的函数(t∈R),
g(t)=f(x)+
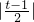 =-xt+
=-xt+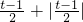 +x3=
+x3=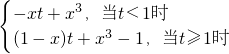 的最小值.
的最小值.由于-x≤0,当t∈(-∞,1)时,g′(t)≤0;由于1-x≥0,故当t∈(1,+∞)时,g′(t)≥0.
考虑到g(t)在t=1处连续,∴g(t)的最小值h(x)=x3-x.
下面再求关于x的函数h(x)=x3-x在x∈[0,1]时的最小值.
h′(x)=3x2-1,令h′(x)=0,解得
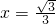 .
.当
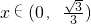 时,h′(x)<0,函数h(x)在此区间上单调递减;当
时,h′(x)<0,函数h(x)在此区间上单调递减;当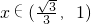 时,h′(x)>0,函数h(x)在此区间上单调递增.
时,h′(x)>0,函数h(x)在此区间上单调递增.故h(x)的最小值为
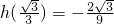 .
.综上可得:当x∈(0,1)时,且t∈R.
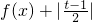 的最小值m=-
的最小值m=-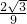 ,即得h的最小值为-m=
,即得h的最小值为-m=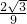 .
.分析:(1)对t分类讨论,利用导数与单调性的关系即可得出;
(2)把问题正确等价转化,通过分类讨论,利用导数研究函数的单调性和最值,即可得出.
点评:熟练掌握分类讨论的思想方法、利用导数研究函数单调性、极值、最值、及把问题正确等价转化是解题的关键.

练习册系列答案
相关题目
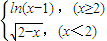 ,F(x)=f(x)-kx.
,F(x)=f(x)-kx. ,求证:F(x)=0有三个不同的实根.
,求证:F(x)=0有三个不同的实根.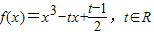 .
.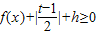 恒成立.
恒成立.