题目内容
已知函数f（x）=ax3+2bx2-3x的极值点是x=1和x=-1．
（1）求a，b的值；
（2）求过点A（1，-2）的曲线y=f（x）的切线方程．
解：（1）求导函数，可得f′（x）=3ax2+4bx-3
∵函数f（x）=ax3+2bx2-3x的极值点是x=1和x=-1．
∴f′（1）=f′（-1）=0
∴
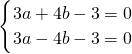，∴a=1，b=0
此时f′（x）=3x2-3=3（x+1）（x-1），可知x=1和x=-1是函数f（x）=ax3+2bx2-3x的极值点；
（2）设切点为P（x0，f（x0） ），则f′（x0）=3x0-3，∴切线方程为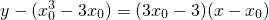
即y=3（x0-1）x+x03-3
∵点A（1，-2）在切线上，
∴-2=3（x0-1）+x03-3
即x03-3+3x0-1=0
∴x0=1，
∴切线方程是y=-2
分析：（1）求导函数，利用函数f（x）=ax3+2bx2-3x的极值点是x=1和x=-1，建立方程组，即可求得a，b的值；
（2）假设切点坐标，写出切线方程，将点A的坐标代入，即可求得过点A（1，-2）的曲线y=f（x）的切线方程．
点评：本题考查导数知识的运用，考查导数的几何意义与函数的极值，解题的关键是理解导数的几何意义及极值的含义．
∵函数f（x）=ax3+2bx2-3x的极值点是x=1和x=-1．
∴f′（1）=f′（-1）=0
∴
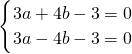，∴a=1，b=0此时f′（x）=3x2-3=3（x+1）（x-1），可知x=1和x=-1是函数f（x）=ax3+2bx2-3x的极值点；
（2）设切点为P（x0，f（x0） ），则f′（x0）=3x0-3，∴切线方程为
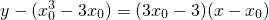
即y=3（x0-1）x+x03-3
∵点A（1，-2）在切线上，
∴-2=3（x0-1）+x03-3
即x03-3
+3x0-1=0∴x0=1，
∴切线方程是y=-2
分析：（1）求导函数，利用函数f（x）=ax3+2bx2-3x的极值点是x=1和x=-1，建立方程组，即可求得a，b的值；
（2）假设切点坐标，写出切线方程，将点A的坐标代入，即可求得过点A（1，-2）的曲线y=f（x）的切线方程．
点评：本题考查导数知识的运用，考查导数的几何意义与函数的极值，解题的关键是理解导数的几何意义及极值的含义．
练习册系列答案
相关题目