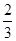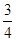题目内容
一袋中有5个白球，3个红球，现从袋中往外取球，每次任取一个记下颜色后放回，直到红球出现10次时停止，设停止时共取了ξ次球，则P(ξ＝12)＝( )
A． ( )10( )2 | B． ()9()2× |
| C．()9()2 | D．()9()2 |
B
解析
练习册系列答案
相关题目
已知服从正态分布
的随机变量在区间
，
和
内取值的概率分别为68.3%，95.4%和99.7%．某校高一年级1000名学生的某次考试成绩服从正态分布
，则此次成绩在（60，120）范围内的学生大约有（ ）
| A．997人 | B．972人 | C．954人 | D．683人 |
如图，矩形OABC内的阴影部分由曲线f(x)＝sinx(x∈(0，π))及直线x＝a(a∈(0，π))与x轴围成，向矩形OABC内随机投掷一点，若落在阴影部分的概率为
，则a的值为( )
A． | B． | C． | D． |
[2014·承德模拟]从装有2个红球和2个白球的口袋内任取2个球，那么互斥但不对立的两个事件是( )
| A．至少有1个白球，都是白球 |
| B．至少有1个白球，至少有1个红球 |
| C．恰有1个白球，恰有2个白球 |
| D．至少有1个白球，都是红球 |