题目内容
设函数f(x)=x2+bln(x+1),其中b≠0.
(Ⅰ)当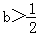 时,判断函数f(x)在定义域上的单调性;
时,判断函数f(x)在定义域上的单调性;
(Ⅱ)求函数f(x)的极值点;
(Ⅲ)证明对任意的正整数n,不等式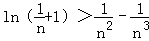 都成立.
都成立.
(Ⅰ)当
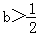 时,判断函数f(x)在定义域上的单调性;
时,判断函数f(x)在定义域上的单调性;(Ⅱ)求函数f(x)的极值点;
(Ⅲ)证明对任意的正整数n,不等式
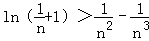 都成立.
都成立.解:(Ⅰ)函数f(x)=x2+bln(x+1)的定义域在(﹣1,+∞)
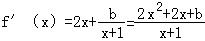
令g(x)=2x2+2x+b,
则g(x)在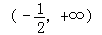 上递增,在
上递增,在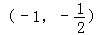 上递减,
上递减,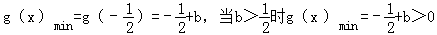
g(x)=2x2+2x+b>0在(﹣1,+∞)上恒成立,
所以f'(x)>0即当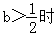 ,函数f(x)在定义域(﹣1,+∞)上单调递增.
,函数f(x)在定义域(﹣1,+∞)上单调递增.
(Ⅱ)(1)由(Ⅰ)知当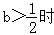 函数f(x)无极值点
函数f(x)无极值点
(2)当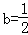 时,
时,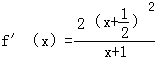 ,
,
∴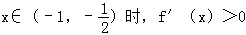
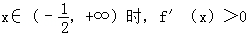 ,
,
∴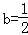 时,函数f(x)在(﹣1,+∞)上无极值点
时,函数f(x)在(﹣1,+∞)上无极值点
(3)当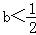 时,解f'(x)=0得两个不同解
时,解f'(x)=0得两个不同解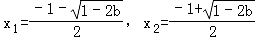
当b<0时,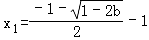
∴x1∈(﹣1,+∞),x2∈(﹣1,+∞),
此时f(x)在(﹣1,+∞)上有唯一的极小值点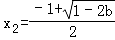
当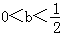 时,x1,x2∈(﹣1,+∞)f'(x)在(﹣1,x1),(x2,+∞)都大于0,f'(x)在(x1,x2)上小于0,
时,x1,x2∈(﹣1,+∞)f'(x)在(﹣1,x1),(x2,+∞)都大于0,f'(x)在(x1,x2)上小于0,
此时f(x)有一个极大值点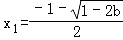 和一个极小值点
和一个极小值点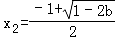
综上可知,b<0,时,f(x)在(﹣1,+∞)上有唯一的极小值点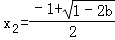
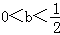 时,f(x)有一个极大值点
时,f(x)有一个极大值点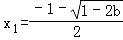 和一个极小值点
和一个极小值点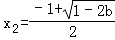
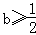 时,函数f(x)在(﹣1,+∞)上无极值点.
时,函数f(x)在(﹣1,+∞)上无极值点.
(Ⅲ)当b=﹣1时,f(x)=x2﹣ln(x+1).令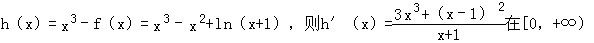 上恒正
上恒正
∴h(x)在[0,+∞)上单调递增,
当x∈(0,+∞)时,恒有h(x)>h(0)=0
即当x∈(0,+∞)时,有x3﹣x2+ln(x+1)>0,ln(x+1)>x2﹣x3,对任意正整数n,取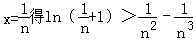
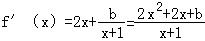
令g(x)=2x2+2x+b,
则g(x)在
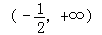 上递增,在
上递增,在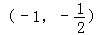 上递减,
上递减,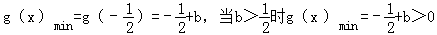
g(x)=2x2+2x+b>0在(﹣1,+∞)上恒成立,
所以f'(x)>0即当
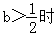 ,函数f(x)在定义域(﹣1,+∞)上单调递增.
,函数f(x)在定义域(﹣1,+∞)上单调递增.(Ⅱ)(1)由(Ⅰ)知当
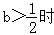 函数f(x)无极值点
函数f(x)无极值点(2)当
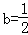 时,
时,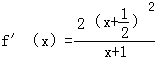 ,
,∴
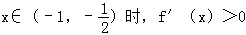
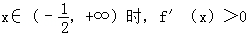 ,
,∴
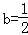 时,函数f(x)在(﹣1,+∞)上无极值点
时,函数f(x)在(﹣1,+∞)上无极值点(3)当
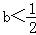 时,解f'(x)=0得两个不同解
时,解f'(x)=0得两个不同解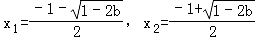
当b<0时,
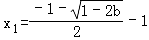
∴x1∈(﹣1,+∞),x2∈(﹣1,+∞),
此时f(x)在(﹣1,+∞)上有唯一的极小值点
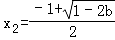
当
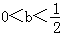 时,x1,x2∈(﹣1,+∞)f'(x)在(﹣1,x1),(x2,+∞)都大于0,f'(x)在(x1,x2)上小于0,
时,x1,x2∈(﹣1,+∞)f'(x)在(﹣1,x1),(x2,+∞)都大于0,f'(x)在(x1,x2)上小于0,此时f(x)有一个极大值点
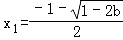 和一个极小值点
和一个极小值点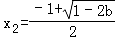
综上可知,b<0,时,f(x)在(﹣1,+∞)上有唯一的极小值点
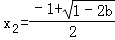
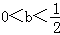 时,f(x)有一个极大值点
时,f(x)有一个极大值点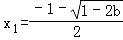 和一个极小值点
和一个极小值点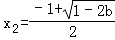
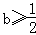 时,函数f(x)在(﹣1,+∞)上无极值点.
时,函数f(x)在(﹣1,+∞)上无极值点.(Ⅲ)当b=﹣1时,f(x)=x2﹣ln(x+1).令
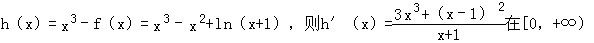 上恒正
上恒正∴h(x)在[0,+∞)上单调递增,
当x∈(0,+∞)时,恒有h(x)>h(0)=0
即当x∈(0,+∞)时,有x3﹣x2+ln(x+1)>0,ln(x+1)>x2﹣x3,对任意正整数n,取
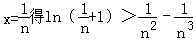

练习册系列答案
相关题目