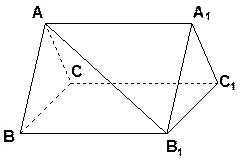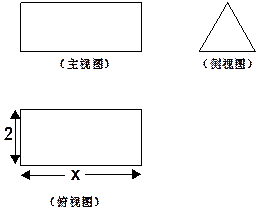题目内容
(本小题满分12分)
如图,三棱柱 中,
中, .
.
(1)求证: ;
;
(2)若 ,问
,问 为何值时,三棱柱
为何值时,三棱柱 体积最大,并求此最大值。
体积最大,并求此最大值。
(1)详见解析,(2) 时,体积
时,体积 取到最大值
取到最大值
解析试题分析:(1)证明线线垂直,一般利用线面垂直判定及性质定理进行多次转化证明. 由 知
知 ,又
,又 ,故
,故 平面
平面 即
即 ,又
,又 ,所以
,所以 (2)研究三棱柱体积,关键明确底面上的高,本题由(1)知:
(2)研究三棱柱体积,关键明确底面上的高,本题由(1)知: 平面
平面 因此将三棱柱体积转化为等高同底的三棱锥
因此将三棱柱体积转化为等高同底的三棱锥 体积(三倍关系),而三棱锥
体积(三倍关系),而三棱锥 体积又等于三棱锥
体积又等于三棱锥 体积,三棱锥
体积,三棱锥 体积等于
体积等于 ,设
,设 不难计算
不难计算 三棱柱
三棱柱 的体积为
的体积为 ,故当
,故当 时,即
时,即 时,体积
时,体积 取到最大值
取到最大值
试题解析:
(1)证明:由 知
知 ,又
,又 ,故
,故 平面
平面 即
即 ,又
,又 ,所以
,所以 (2)设
(2)设 在
在 中
中 同理
同理 在
在 中,
中,  ,所以
,所以 从而三棱柱
从而三棱柱 的体积为
的体积为 因
因 故当
故当 时,即
时,即 时,体积
时,体积 取到最大值
取到最大值
考点:线面垂直判定与性质定理,三棱柱的体积

练习册系列答案
相关题目
 BCD的三条高线的交点;
BCD的三条高线的交点;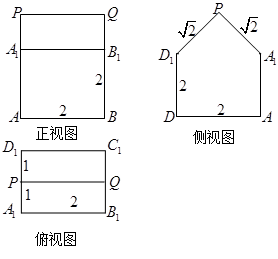
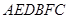 的直观图及三视图如图所示,
的直观图及三视图如图所示,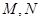 分别为
分别为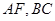 的中点.
的中点.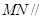 平面
平面 ;
;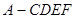 的体积.
的体积.
 ,
,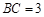 ,过动点A作
,过动点A作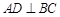 ,垂足D在线段BC上且异于点B,连接AB,沿
,垂足D在线段BC上且异于点B,连接AB,沿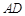 将△
将△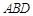 折起,使
折起,使 (如图2所示).
(如图2所示).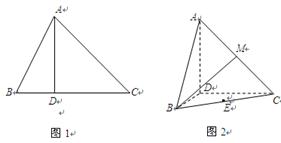
 的长为多少时,三棱锥
的长为多少时,三棱锥 的体积最大;
的体积最大; ,
,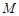 分别为棱
分别为棱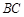 ,
,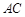 的中点,试在棱
的中点,试在棱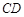 上确定一点
上确定一点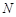 ,使得
,使得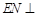
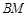 ,并求
,并求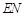 与平面
与平面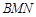 所成角的大小.
所成角的大小. 中,
中, ,则
,则 两点间的球面距离为 .
两点间的球面距离为 .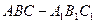 的直观图和三视图如下图所示,其侧视图为正三角形(单位cm)
的直观图和三视图如下图所示,其侧视图为正三角形(单位cm)