题目内容
设数列{an}是等比数列,其前n项和为Sn,且S3=3a3,则公比q的值为( )A.-

B.

C.1或-

D.1或

【答案】分析:分两种情况:当q=1时,得到此等比数列为常数列,各项都等于第一项,已知的等式显然成立;当q=不等于1时,利用等比数列的前n项和的公式及等比数列的通项公式公式化简已知的等式,得到关于q的方程,根据q不等于解出q的值,综上,得到所有满足题意的等比q的值.
解答:解:当q=1时,S3=a1+a2+a3=3a1=3a3,成立;
当q≠1时,得到S3=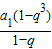 ,a3=a1q2,又S3=3a3,
,a3=a1q2,又S3=3a3,
所以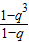 =3q2,
=3q2,
化简得:2q2-q-1=0,即(q-1)(2q+1)=0,
由q≠1即q-1≠0,解得q=- .
.
综上,公比q的值为1或- .
.
故选C.
点评:此题考查学生掌握等比数列的性质,灵活运用等比数列的通项公式及前n项和的公式化简求值,是一道综合题.
解答:解:当q=1时,S3=a1+a2+a3=3a1=3a3,成立;
当q≠1时,得到S3=
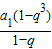 ,a3=a1q2,又S3=3a3,
,a3=a1q2,又S3=3a3,所以
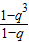 =3q2,
=3q2,化简得:2q2-q-1=0,即(q-1)(2q+1)=0,
由q≠1即q-1≠0,解得q=-
 .
.综上,公比q的值为1或-
 .
.故选C.
点评:此题考查学生掌握等比数列的性质,灵活运用等比数列的通项公式及前n项和的公式化简求值,是一道综合题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目