题目内容
已知f(x)是定义在(0,+∞)上的单调递增函数,且对定义域内任意x,y都有f(x·y)=f(x)+f(y)且f(2)=1,求使不等式f(x)+f(x-3)≤2成立的x的取值范围.
解析:这是抽象函数单调性的应用,解题的关键在于处理好f(x·y)=f(x)+f(y)和f(x)+f(x-3)≤2这两个式子,并且要能够将f(x)+f(x-3)≤2转化成与函数的单调性有关.
解:∵f(x)是定义在(0,+∞)上的单调递增函数,
∴x>3且f(x·y)=f(x)+f(y) ,
∴f(x)+f(x-3)=f(x2-3x),
且x>3,2=f(2)+f(2)=f(4).
因此f(x)+f(x-3)≤2f(x2-3x)≤f(4),
即
![]() 3<x≤4.
3<x≤4.
所以x的取值范围是(3,4].

练习册系列答案
相关题目
 ) =
f(x)-f(y)
) =
f(x)-f(y) 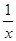 ) <2
) <2  ∪
∪ 上的奇函数,当
上的奇函数,当 时,f (x)的图象如图所示,那么f (x)的值域是
时,f (x)的图象如图所示,那么f (x)的值域是
