Question

（2010•台州二模）已知ABCD为平行四边形，AB=2，BC=2

2

，∠ABC=45°，BEFC是长方形，S是EF的中点，BE=

5

，平面BEFC⊥平面ABCD，

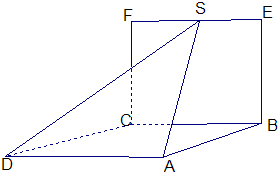
（Ⅰ）求证：SA⊥BC；
（Ⅱ）求直线SD与平面BEFC所成角的正切值．

Answer 1

分析：（Ⅰ）作SM⊥BC于M点，连接MA，因为S是EF的中点，所以MB=

2

，由AB=2，∠ABC=45°，知AM⊥BC，由此能够证明SA⊥BC．
（Ⅱ）作DN⊥BC于N点，连接SN，由平面BEFC⊥平面ABCD，知DN⊥面BEFC，所以∠DSN是SD与面BEFC所成的角，由此能求出直线SD与平面BEFC所成角的正切值．

解答：解：（Ⅰ）作SM⊥BC于M点，连接MA，
∵ABCD为平行四边形，BEFC是长方形，BC=2

2

，S是EF的中点，
∴MB=

2

，
∵AB=2，BC=2

2

，∠ABC=45°，
∴AC=

4+8-2×2×2 2 ×sin45°

=2，
∴∠BAC=90°，
∴AM=

1

2

BC=

2

，
∴AM⊥BC，
∴BC⊥面SMA，
∴SA⊥BC…（7分）
（Ⅱ）作DN⊥BC于N点，连接SN，
∵平面BEFC⊥平面ABCD，BE=

5

，
∴DN⊥面BEFC，DN=AM=

2

，SN=

SM2+MN2

=

5+8

=

13

，
∴∠DSN是SD与面BEFC所成的角，
∵DN=

2

，SN=

13

∴tan∠DSN=

DN

SN

=

2

13

=

26

13

，
所以直线SD与平面BEFC所成角的正切值为

26

13

．…（14分）

点评：本题考查异面直线互相垂直的证明和直线与平面所成角的正切值的求法，是基础题，解题时要认真审题，仔细解答．