题目内容
某小区要建一个面积为500平方米的矩形绿地，四周有小路，绿地长边外路宽5米，短边外路宽9米，怎样设计绿地的长与宽，使绿地和小路所占的总面积最小，并求出最小值．
【答案】分析：若设绿地长边为x米，则宽为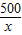
米，总面积
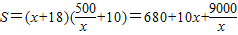；利用基本不等式a+b≥2
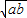（a＞0，b＞0），可求得总面积的最小值及对应的绿地的长与宽．
解答：
解：设绿地长边为x米，则宽为
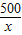米，
总面积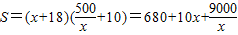
；
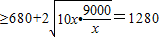当且仅当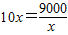
，即x=30时，上式取等号；
所以，绿地的长为30米，宽为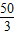
米时，绿地和小路所占的总面积最小，最小值为1280平方米．
点评：本题利用矩形的面积公式，考查了基本不等式a+b≥2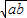
（其中a＞0，b＞0）的应用，是基础题．
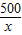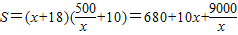米，总面积；利用基本不等式a+b≥2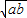（a＞0，b＞0），可求得总面积的最小值及对应的绿地的长与宽．解答：
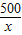解：设绿地长边为x米，则宽为米，总面积
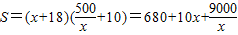
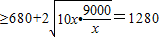；当且仅当
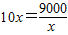，即x=30时，上式取等号；所以，绿地的长为30米，宽为
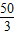米时，绿地和小路所占的总面积最小，最小值为1280平方米．点评：本题利用矩形的面积公式，考查了基本不等式a+b≥2
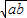（其中a＞0，b＞0）的应用，是基础题． 
练习册系列答案
阅读快车系列答案
相关题目
某小区要建一个面积为500平方米的矩形绿地，四周有小路，绿地长边外路宽5米，短边外路宽9米，怎样设计绿地的长与宽，使绿地和小路所占的总面积最小，并求出最小值．
